38 Mathematical problems

Alhazen's problem, also known as Alhazen's billiard problem, is a mathematical problem in geometrical optics first formulated by Ptolemy in 150 AD. It is named for the 11th-century Arab mathematician Alhazen who presented a geometric solution in his Book of Optics. The algebraic solution involves quartic equations and was found in 1965 by Jack M. Elkin.

Angle trisection is a classical problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.

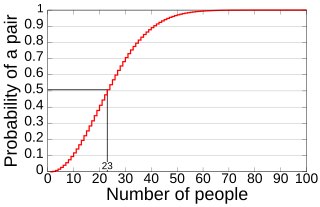
In probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. In a group of 23 people, the probability of a shared birthday is 50%, while a group of 70 has a 99.9% chance of a shared birthday.

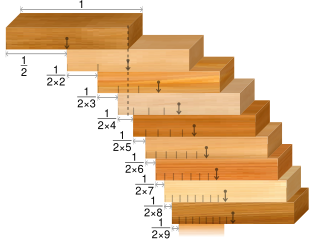
In statics, the block-stacking problem is a puzzle concerning the stacking of blocks at the edge of a table.

In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions.

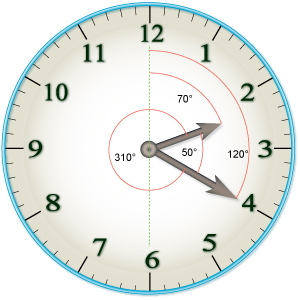
Clock angle problems are a type of mathematical problem which involve finding the angle between the hands of an analog clock.

Doubling the cube, also known as the Delian problem, is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first. As with the related problems of squaring the circle and trisecting the angle, doubling the cube is now known to be impossible using only a compass and straightedge, but even in ancient times solutions were known that employed other tools.

The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n queens problem of placing n non-attacking queens on an n×n chessboard, for which solutions exist for all natural numbers n with the exception of n = 2 and n = 3.

The firing squad synchronization problem is a problem in computer science and cellular automata in which the goal is to design a cellular automaton that, starting with a single active cell, eventually reaches a state in which all cells are simultaneously active. It was first proposed by John Myhill in 1957 and published in 1962 by Edward Moore.

In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance 1 from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 5, 6 or 7. The correct value may depend on the choice of axioms for set theory.

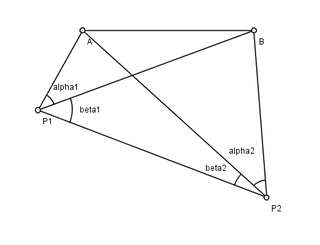
Hansen's problem is a problem in planar surveying, named after the astronomer Peter Andreas Hansen (1795–1874), who worked on the geodetic survey of Denmark. There are two known points A and B, and two unknown points P1 and P2. From P1 and P2 an observer measures the angles made by the lines of sight to each of the other three points. The problem is to find the positions of P1 and P2. See figure; the angles measured are (α1, β1, α2, β2).

The "happy ending problem" is the following statement:Theorem: any set of five points in the plane in general position has a subset of four points that form the vertices of a convex quadrilateral.

Illumination problems are a class of mathematical problems that study the illumination of rooms with mirrored walls by point light sources.

In the field of mathematics known as functional analysis, the invariant subspace problem is a partially unresolved problem asking whether every bounded operator on a complex Banach space sends some non-trivial closed subspace to itself. Many variants of the problem have been solved, by restricting the class of bounded operators considered or by specifying a particular class of Banach spaces. The problem is still open for separable Hilbert spaces.

In computer science and mathematics, the Josephus problem is a theoretical problem related to a certain counting-out game.

Kirkman's schoolgirl problem is a problem in combinatorics proposed by Rev. Thomas Penyngton Kirkman in 1850 as Query VI in The Lady's and Gentleman's Diary (pg.48). The problem states: Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily so that no two shall walk twice abreast.

In computational geometry, Klee's measure problem is the problem of determining how efficiently the measure of a union of (multidimensional) rectangular ranges can be computed. Here, a d-dimensional rectangular range is defined to be a Cartesian product of d intervals of real numbers, which is a subset of Rd.

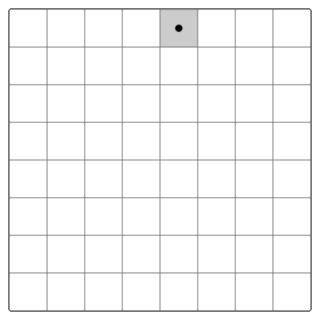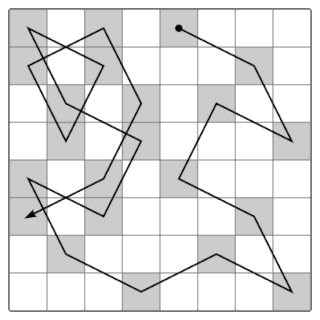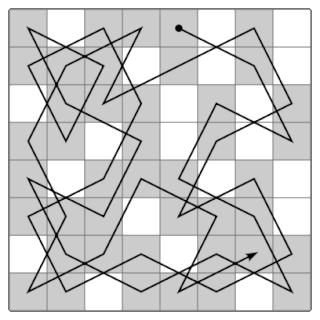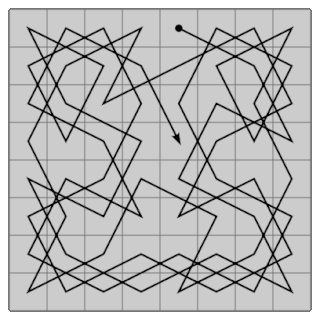
A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square exactly once. If the knight ends on a square that is one knight's move from the beginning square, the tour is closed; otherwise, it is open.

In mathematics, a moment problem arises as the result of trying to invert the mapping that takes a measure μ to the sequences of moments

The Monty Hall problem is a brain teaser, in the form of a probability puzzle, loosely based on the American television game show Let's Make a Deal and named after its original host, Monty Hall. The problem was originally posed in a letter by Steve Selvin to the American Statistician in 1975. It became famous as a question from reader Craig F. Whitaker's letter quoted in Marilyn vos Savant's "Ask Marilyn" column in Parade magazine in 1990:Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?

In mathematics, the mountain climbing problem is a problem of finding the conditions that two functions forming profiles of a two-dimensional mountain must satisfy, so that two climbers can start on the bottom on the opposite sides of the mountain and coordinate their movements to meet while always staying at the same height. This problem was named and posed in this form by James V. Whittaker (1966), but its history goes back to Tatsuo Homma (1952), who solved a version of it. The problem has been repeatedly rediscovered and solved independently in different context by a number of people.

Mrs. Miniver's problem is a geometry problem about circles. Given a circle A, find a circle B such that the area of the lens formed by intersecting their two interiors is equal to the area of the symmetric difference of A and B.

In geometry, the napkin-ring problem involves finding the volume of a "band" of specified height around a sphere, i.e. the part that remains after a hole in the shape of a circular cylinder is drilled through the center of the sphere. It is a counterintuitive fact that this volume does not depend on the original sphere's radius but only on the resulting band's height.

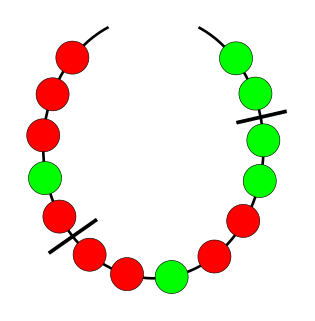
Necklace splitting is a picturesque name given to several related problems in combinatorics and measure theory. Its name and solutions are due to mathematicians Noga Alon and Douglas B. West.

In mathematics, in the area of discrete geometry, the no-three-in-line problem asks for the maximum number of points that can be placed in the n × n grid so that no three points are collinear. This number is at most 2n, since if 2n + 1 points are placed in the grid, then by the pigeonhole principle some row and some column will contain three points. The problem was introduced by Henry Dudeney in 1917.

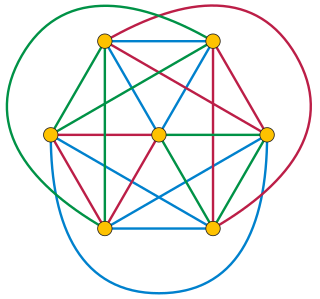
The Oberwolfach problem is an unsolved problem in mathematics that may be formulated either as a problem of scheduling seating assignments for diners, or more abstractly as a problem in graph theory, on the edge cycle covers of complete graphs. It is named after the Mathematical Research Institute of Oberwolfach, where the problem was posed in 1967 by Gerhard Ringel.

In discrete geometry, the original orchard-planting problem asks for the maximum number of 3-point lines attainable by a configuration of a specific number of points in the plane. It is also called the tree-planting problem or simply the orchard problem. There are also investigations into how many k-point lines there can be. Hallard T. Croft and Paul Erdős proved tk > c n2 / k3, where n is the number of points and tk is the number of k-point lines. Their construction contains some m-point lines, where m > k. One can also ask the question if these are not allowed.

In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who experimented with soap films. The problem is considered part of the calculus of variations. The existence and regularity problems are part of geometric measure theory.

Regiomontanus' angle maximization problem

In mathematics, the Regiomontanus's angle maximization problem, is a famous optimization problem posed by the 15th-century German mathematician Johannes Müller. The problem is as follows:

The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1736 laid the foundations of graph theory and prefigured the idea of topology.

The Snellius–Pothenot problem is a problem in planar surveying. Given three known points A, B and C, an observer at an unknown point P observes that the segment AC subtends an angle and the segment CB subtends an angle ; the problem is to determine the position of the point P..

In geometry, a square trisection consists of cutting a square into pieces that can be rearranged to form three identical squares.

Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a square.

Squaring the square is the problem of tiling an integral square using only other integral squares. The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares.

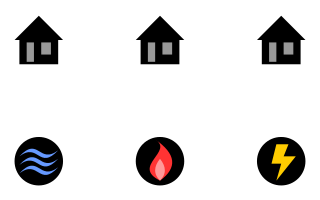
The classical mathematical puzzle known as the three utilities problem; the three cottages problem or sometimes water, gas and electricity can be stated as follows:Suppose there are three cottages on a plane and each needs to be connected to the water, gas, and electricity companies. Without using a third dimension or sending any of the connections through another company or cottage, is there a way to make all nine connections without any of the lines crossing each other?

In the mathematics of graph drawing, Turán's brick factory problem asks for the minimum number of crossings in a drawing of a complete bipartite graph. The problem is named after Pál Turán, who formulated it while being forced to work in a brick factory during World War II.

Water pouring puzzles are a class of puzzle involving a finite collection of water jugs of known integer capacities . Initially each jug contains a known integer volume of liquid, not necessarily equal to its capacity. Puzzles of this type ask how many steps of pouring water from one jug to another are needed to reach a goal state, specified in terms of the volume of liquid that must be present in some jug or jugs.

In number theory, Znám's problem asks which sets of k integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other mathematicians had considered similar problems around the same time. One closely related problem drops the assumption of properness of the divisor, and will be called the improper Znám problem hereafter.