45 Conjectures

In mathematics, a conjecture is a conclusion or a proposition which is suspected to be true due to preliminary supporting evidence, but for which no proof or disproof has yet been found. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.

List of unsolved problems in mathematics

Since the Renaissance, every century has seen the solution of more mathematical problems than the century before, yet many mathematical problems, both major and minor, still remain unsolved. These unsolved problems occur in multiple domains, including physics, computer science, algebra, analysis, combinatorics, algebraic, differential, discrete and Euclidean geometries, graph, group, model, number, set and Ramsey theories, dynamical systems, partial differential equations, and more. Some problems may belong to more than one discipline of mathematics and be studied using techniques from different areas. Prizes are often awarded for the solution to a long-standing problem, and lists of unsolved problems receive considerable attention.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is an edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.

The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé (1988) and David Masser (1985). It is stated in terms of three positive integers, a, b and c that are relatively prime and satisfy a + b = c. If d denotes the product of the distinct prime factors of abc, the conjecture essentially states that d is usually not much smaller than c. In other words: if a and b are composed from large powers of primes, then c is usually not divisible by large powers of primes. A number of famous conjectures and theorems in number theory would follow immediately from the abc conjecture or its versions. Goldfeld (1996) described the abc conjecture as "the most important unsolved problem in Diophantine analysis".

In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of his many conjectures in graph coloring theory. The conjecture states that, among all graphs requiring colors, the complete graph is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than , then, according to the conjecture, it may be colored with fewer than colors.

In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex.

M-theory is a theory in physics that unifies all consistent versions of superstring theory. Edward Witten first conjectured the existence of such a theory at a string-theory conference at the University of Southern California in the spring of 1995. Witten's announcement initiated a flurry of research activity known as the second superstring revolution.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings into a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

In mathematics, a finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. Subdivision rules in a sense are generalizations of regular geometric fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals. Subdivision rules have been used in architecture, biology, and computer science, as well as in the study of hyperbolic manifolds. Substitution tilings are a well-studied type of subdivision rule.

In mathematics, the Casas-Alvero conjecture is an open problem about polynomials which have factors in common with their derivatives, proposed by Eduardo Casas-Alvero in 2001.

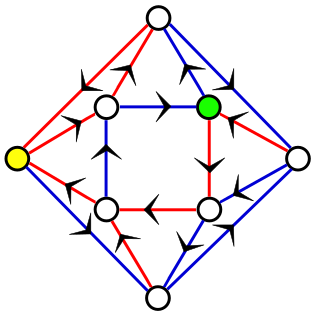
In the mathematics of graph coloring, Cereceda’s conjecture is an unsolved problem on the distance between pairs of colorings of sparse graphs. It states that, for two different colorings of a graph of degeneracy d, both using at most d + 2 colors, it should be possible to reconfigure one coloring into the other by changing the color of one vertex at a time, using a number of steps that is quadratic in the size of the graph. The conjecture is named after Luis Cereceda, who formulated it in his 2007 doctoral dissertation.

In computer science, more precisely, in the theory of deterministic finite automata (DFA), a synchronizing word or reset sequence is a word in the input alphabet of the DFA that sends any state of the DFA to one and the same state. That is, if an ensemble of copies of the DFA are each started in different states, and all of the copies process the synchronizing word, they will all end up in the same state. Not every DFA has a synchronizing word; for instance, a DFA with two states, one for words of even length and one for words of odd length, can never be synchronized.

In mathematics, monstrous moonshine, or moonshine theory, is the unexpected connection between the monster group M and modular functions, in particular, the j function. The term was coined by John Conway and Simon P. Norton in 1979.

In graph-theoretic mathematics, a cycle double cover is a collection of cycles in an undirected graph that together include each edge of the graph exactly twice. For instance, for any polyhedral graph, the faces of a convex polyhedron that represents the graph provide a double cover of the graph: each edge belongs to exactly two faces.

Pierre René, Viscount Deligne is a Belgian mathematician. He is best known for work on the Weil conjectures, leading to a complete proof in 1973. He is the winner of the 2013 Abel Prize, 2008 Wolf Prize, 1988 Crafoord Prize, and 1978 Fields Medal.

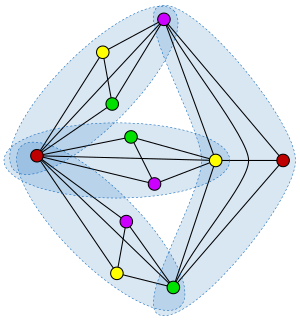
In graph theory, the Erdős–Faber–Lovász conjecture is an unsolved problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:If k complete graphs, each having exactly k vertices, have the property that every pair of complete graphs has at most one shared vertex, then the union of the graphs can be properly colored with k colors.

In graph theory, the unproven Erdős–Gyárfás conjecture, made in 1995 by the prolific mathematician Paul Erdős and his collaborator András Gyárfás, states that every graph with minimum degree 3 contains a simple cycle whose length is a power of two. Erdős offered a prize of $100 for proving the conjecture, or $50 for a counterexample; it is one of many conjectures of Erdős.

The "happy ending problem" is the following statement:Theorem: any set of five points in the plane in general position has a subset of four points that form the vertices of a convex quadrilateral.

Kefeng Liu, is a Chinese-American mathematician who is known for his contributions to geometric analysis, particularly the geometry, topology and analysis of moduli spaces of Riemann surfaces and Calabi-Yau manifolds. He is a professor of mathematics at University of California, Los Angeles, as well as the Executive Director of the Center of Mathematical Sciences at Zhejiang University. He is best-known for his collaboration with Bong Lian and Shing-Tung Yau in which they establish some enumerative geometry conjectures motivated by mirror symmetry.

In graph theory, a graceful labeling of a graph with m edges is a labeling of its vertices with some subset of the integers between 0 and m inclusive, such that no two vertices share a label, and each edge is uniquely identified by the absolute difference between its endpoints, such that this magnitude lies between 1 and m inclusive. A graph which admits a graceful labeling is called a graceful graph.

In combinatorial geometry, the Hadwiger conjecture states that any convex body in n-dimensional Euclidean space can be covered by 2n or fewer smaller bodies homothetic with the original body, and that furthermore, the upper bound of 2n is necessary if and only if the body is a parallelepiped. There also exists an equivalent formulation in terms of the number of floodlights needed to illuminate the body.

In graph theory, the Hadwiger conjecture states that if G is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

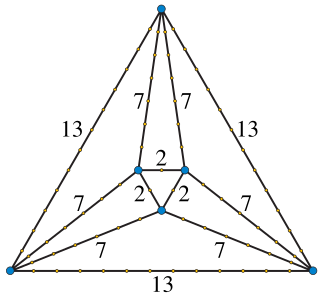
In mathematics, Harborth's conjecture states that every planar graph has a planar drawing in which every edge is a straight segment of integer length. This conjecture is named after Heiko Harborth, and would strengthen Fáry's theorem on the existence of straight-line drawings for every planar graph. For this reason, a drawing with integer edge lengths is also known as an integral Fáry embedding. Despite much subsequent research, Harborth's conjecture remains unsolved.

In mathematical programming and polyhedral combinatorics, the Hirsch conjecture is the statement that the edge-vertex graph of an n-facet polytope in d-dimensional Euclidean space has diameter no more than n − d. That is, any two vertices of the polytope must be connected to each other by a path of length at most n − d. The conjecture was first put forth in a letter by Warren M. Hirsch to George B. Dantzig in 1957 and was motivated by the analysis of the simplex method in linear programming, as the diameter of a polytope provides a lower bound on the number of steps needed by the simplex method. The conjecture is now known to be false in general.

In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.

In mathematics, a Littlewood polynomial is a polynomial all of whose coefficients are +1 or −1. Littlewood's problem asks how large the values of such a polynomial must be on the unit circle in the complex plane. The answer to this would yield information about the autocorrelation of binary sequences. They are named for J. E. Littlewood who studied them in the 1950s.

In number theory, and especially the study of diophantine approximation, the lonely runner conjecture is a conjecture originally due to J. M. Wills in 1967. Applications of the conjecture are widespread in mathematics; they include view obstruction problems and calculating the chromatic number of distance graphs and circulant graphs. The conjecture was given its picturesque name by L. Goddyn in 1998.

In theoretical physics, the anti-de Sitter/conformal field theory correspondence, sometimes called Maldacena duality or gauge/gravity duality, is a conjectured relationship between two kinds of physical theories. On one side are anti-de Sitter spaces (AdS) which are used in theories of quantum gravity, formulated in terms of string theory or M-theory. On the other side of the correspondence are conformal field theories (CFT) which are quantum field theories, including theories similar to the Yang–Mills theories that describe elementary particles.

In mathematics, the Manin conjecture describes the conjectural distribution of rational points on an algebraic variety relative to a suitable height function. It was proposed by Yuri I. Manin and his collaborators in 1989 when they initiated a program with the aim of describing the distribution of rational points on suitable algebraic varieties.

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery (1973) that the pair correlation between pairs of zeros of the Riemann zeta function is

In mathematics, in the area of discrete geometry, the no-three-in-line problem asks for the maximum number of points that can be placed in the n × n grid so that no three points are collinear. This number is at most 2n, since if 2n + 1 points are placed in the grid, then by the pigeonhole principle some row and some column will contain three points. The problem was introduced by Henry Dudeney in 1917.

The P versus NP problem is a major unsolved problem in computer science. It asks whether every problem whose solution can be quickly verified can also be solved quickly.

In mathematics, the Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.

The Ryu–Takayanagi conjecture is a conjecture within holography that posits a quantitative relationship between the entanglement entropy of a conformal field theory and the geometry of an associated anti-de Sitter spacetime. The formula characterizes "holographic screens" in the bulk; that is, it specifies which regions of the bulk geometry are "responsible to particular information in the dual CFT". The conjecture is named after Shinsei Ryu and Tadashi Takayanagi, who jointly published the result in 2006. As a result, the authors were awarded the 2015 New Horizons in Physics Prize for "fundamental ideas about entropy in quantum field theory and quantum gravity". The formula was generalized to a covariant form in 2007.

In mathematics, specifically transcendental number theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.

Sumner's conjecture states that every orientation of every -vertex tree is a subgraph of every -vertex tournament. David Sumner, a graph theorist at the University of South Carolina, conjectured in 1971 that tournaments are universal graphs for polytrees. The conjecture was proven for all large by Daniela Kühn, Richard Mycroft, and Deryk Osthus.

In mathematics, a sunflower or -system is a collection of sets whose pairwise intersection is constant. This constant intersection is called the kernel of the sunflower.

In mathematics, the surface subgroup conjecture of Friedhelm Waldhausen states that the fundamental group of every closed, irreducible 3-manifold with infinite fundamental group has a surface subgroup. By "surface subgroup" we mean the fundamental group of a closed surface not the 2-sphere. This problem is listed as Problem 3.75 in Robion Kirby's problem list.

The SYZ conjecture is an attempt to understand the mirror symmetry conjecture, an issue in theoretical physics and mathematics. The original conjecture was proposed in a paper by Strominger, Yau, and Zaslow, entitled "Mirror Symmetry is T-duality".

In mathematics, Szymanski's conjecture, named after Ted H. Szymanski (1989), states that every permutation on the n-dimensional doubly directed hypercube graph can be routed with edge-disjoint paths. That is, if the permutation σ matches each vertex v to another vertex σ(v), then for each v there exists a path in the hypercube graph from v to σ(v) such that no two paths for two different vertices u and v use the same edge in the same direction.

In number theory and algebraic geometry, the Tate conjecture is a 1963 conjecture of John Tate that would describe the algebraic cycles on a variety in terms of a more computable invariant, the Galois representation on étale cohomology. The conjecture is a central problem in the theory of algebraic cycles. It can be considered an arithmetic analog of the Hodge conjecture.

In graph theory, total coloring is a type of graph coloring on the vertices and edges of a graph. When used without any qualification, a total coloring is always assumed to be proper in the sense that no adjacent edges and no edge and its endvertices are assigned the same color. The total chromatic number χ″(G) of a graph G is the fewest colors needed in any total coloring of G.

In the mathematics of graph drawing, Turán's brick factory problem asks for the minimum number of crossings in a drawing of a complete bipartite graph. The problem is named after Pál Turán, who formulated it while being forced to work in a brick factory during World War II.

A wormhole is a speculative structure linking disparate points in spacetime, and is based on a special solution of the Einstein field equations.