 W
WMathematical puzzles make up an integral part of recreational mathematics. They have specific rules, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that satisfies the given conditions. Mathematical puzzles require mathematics to solve them. Logic puzzles are a common type of mathematical puzzle.
 W
WThe 100 prisoners problem is a mathematical problem in probability theory and combinatorics. In this problem, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive. The rules state that each prisoner may open only 50 drawers and cannot communicate with other prisoners. At first glance, the situation appears hopeless, but a clever strategy offers the prisoners a realistic chance of survival. Danish computer scientist Peter Bro Miltersen first proposed the problem in 2003.
 W
WIn recreational mathematics, an almost integer is any number that is not an integer but is very close to one. Almost integers are considered interesting when they arise in some context in which they are unexpected.
 W
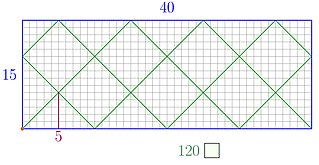
WIn recreational mathematics, arithmetic billiards provide a geometrical method to determine the least common multiple and the greatest common divisor of two natural numbers by making use of reflections inside a rectangle whose sides are the two given numbers. This is an easy example of trajectory analysis of dynamical billiards.
 W
WThe Bedlam cube is a solid dissection puzzle invented by British puzzle expert Bruce Bedlam.
 W
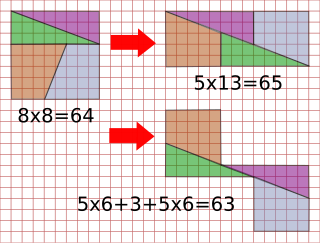
WThe chessboard paradox or paradox of Loyd and Schlömilch is a falsidical paradox based on an optical illusion. A chessboard or a square with a side length of 8 units is cut into four pieces. Those four pieces are used to form a rectangle with side lengths of 13 and 5 units. Hence the combined area of all four pieces is 64 area units in the square but 65 area units in the rectangle, this seeming contradiction is due an optical illusion as the four pieces don't fit exactly in the rectangle, but leave a small barely visible gap around the rectangle's diagonal. The paradox is sometimes attributed to the American puzzle inventor Sam Loyd (1841–1911) and the German mathematician Oskar Schlömilch (1832–1901)
 W
WThe coin problem is a mathematical problem that asks for the largest monetary amount that cannot be obtained using only coins of specified denominations. For example, the largest amount that cannot be obtained using only coins of 3 and 5 units is 7 units. The solution to this problem for a given set of coin denominations is called the Frobenius number of the set. The Frobenius number exists as long as the set of coin denominations has no common divisor greater than 1.
 W
WConway's puzzle, or blocks-in-a-box, is a packing problem using rectangular blocks, named after its inventor, mathematician John Conway. It calls for packing thirteen 1 × 2 × 4 blocks, one 2 × 2 × 2 block, one 1 × 2 × 2 block, and three 1 × 1 × 3 blocks into a 5 × 5 × 5 box.
 W
WDisentanglement puzzles are a type or group of mechanical puzzle that involves disentangling one piece or set of pieces from another piece or set of pieces. Several subtypes are included under this category, the names of which are sometimes used synonymously for the group: wire puzzles; nail puzzles; ring-and-string puzzles; et al. Although the initial object is disentanglement, the reverse problem of reassembling the puzzle can be as hard as—or even harder than—disentanglement. There are several different kinds of disentanglement puzzles, though a single puzzle may incorporate several of these features.
 W
WIn geometry, a domino tiling of a region in the Euclidean plane is a tessellation of the region by dominos, shapes formed by the union of two unit squares meeting edge-to-edge. Equivalently, it is a perfect matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.
 W
WAn Egyptian fraction is a finite sum of distinct unit fractions, such as
 W
WThe eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n queens problem of placing n non-attacking queens on an n×n chessboard, for which solutions exist for all natural numbers n with the exception of n = 2 and n = 3.
 W
WEleusis is a shedding-type card game where one player chooses a secret rule to determine which cards can be played on top of others, and the other players attempt to determine the rule using inductive logic.
 W
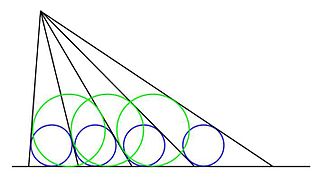
WIn geometry, the equal incircles theorem derives from a Japanese Sangaku, and pertains to the following construction: a series of rays are drawn from a given point to a given line such that the inscribed circles of the triangles formed by adjacent rays and the base line are equal. In the illustration the equal blue circles define the spacing between the rays, as described.
 W
WIn general, exponentiation fails to be commutative. However, the equation holds in special cases, such as
 W
WFibonacci nim is a mathematical subtraction game, a variant of the game of nim. The game was first described by Michael J. Whinihan in 1963, who credits its invention to Robert E. Gaskell. It is called Fibonacci nim because the Fibonacci numbers feature heavily in its analysis.
 W
WIn geometry, flexagons are flat models, usually constructed by folding strips of paper, that can be flexed or folded in certain ways to reveal faces besides the two that were originally on the back and front.
 W
WA geometric magic square, often abbreviated to geomagic square, is a generalization of magic squares invented by Lee Sallows in 2001. A traditional magic square is a square array of numbers whose sum taken in any row, any column, or in either diagonal is the same target number. A geomagic square, on the other hand, is a square array of geometrical shapes in which those appearing in each row, column, or diagonal can be fitted together to create an identical shape called the target shape. As with numerical types, it is required that the entries in a geomagic square be distinct. Similarly, the eight trivial variants of any square resulting from its rotation and/or reflection, are all counted as the same square. By the dimension of a geomagic square is meant the dimension of the pieces it uses. Hitherto interest has focused mainly on 2D squares using planar pieces, but pieces of any dimension are permitted.
 W
WThe game of Go is one of the most popular games in the world. As a result of its elegant and simple rules, the game has long been an inspiration for mathematical research. Shen Kuo, a Chinese scholar in 11th century, estimated that the number of possible board positions is around 10172 in The Dream Pool Essays. In more recent years, research of the game by John H. Conway led to the invention of the surreal numbers and contributed to development of combinatorial game theory (with Go Infinitesimals being a specific example of its use in Go).
 W
WGrundy's game is a two-player mathematical game of strategy. The starting configuration is a single heap of objects, and the two players take turn splitting a single heap into two heaps of different sizes. The game ends when only heaps of size two and smaller remain, none of which can be split unequally. The game is usually played as a normal play game, which means that the last person who can make an allowed move wins.
 W
WThe hexagonal tortoise problem was invented by Korean aristocrat and mathematician Choi Seok-jeong, who lived from 1646 to 1715. It is a mathematical problem that involves a hexagonal lattice, like the hexagonal pattern on some tortoises' shells, to the (N) vertices of which must be assigned integers in such a way that the sum of all integers at the vertices of each hexagon is the same. The problem has apparent similarities to a magic square although it is a vertex-magic format rather than an edge-magic form or the more typical rows-of-cells form.
 W
WA hinged dissection, also known as a swing-hinged dissection or Dudeney dissection, is a kind of geometric dissection in which all of the pieces are connected into a chain by "hinged" points, such that the rearrangement from one figure to another can be carried out by swinging the chain continuously, without severing any of the connections. Typically, it is assumed that the pieces are allowed to overlap in the folding and unfolding process; this is sometimes called the "wobbly-hinged" model of hinged dissection.
 W
WHooper's paradox is a falsidical paradox based on a optical illusion. A geometric shape with an area of 32 units is dissected into four parts, which afterwards get assembled into a rectangle with an area of only 30 units.
 W
WThe Huzita–Justin axioms or Huzita–Hatori axioms are a set of rules related to the mathematical principles of origami, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane, and that all folds are linear. These are not a minimal set of axioms but rather the complete set of possible single folds.
 W
WThe Journal of Recreational Mathematics was an American journal dedicated to recreational mathematics, started in 1968. It had generally been published quarterly by the Baywood Publishing Company, until it ceased publication with the last issue published in 2014. The initial publisher was Greenwood Periodicals.
 W
WKawasaki's theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is flat-foldable if and only if alternatingly adding and subtracting the angles of consecutive folds around the vertex gives an alternating sum of zero. Crease patterns with more than one vertex do not obey such a simple criterion, and are NP-hard to fold.
 W
WThe Kobon triangle problem is an unsolved problem in combinatorial geometry first stated by Kobon Fujimura (1903-1983). The problem asks for the largest number N(k) of nonoverlapping triangles whose sides lie on an arrangement of k lines. Variations of the problem consider the projective plane rather than the Euclidean plane, and require that the triangles not be crossed by any other lines of the arrangement.
 W
WWilliam George Kolakoski, known as Bill to family and friends, was an American artist and recreational mathematician who is most famous for devising and giving his name to the Kolakoski sequence, a self-generating sequence of integers that has been extensively studied by mathematicians since he first described it in the American Mathematical Monthly in 1965.
 W
WMaekawa's theorem is a theorem in the mathematics of paper folding named after Jun Maekawa. It relates to flat-foldable origami crease patterns and states that at every vertex, the numbers of valley and mountain folds always differ by two in either direction. The same result was also discovered by Jacques Justin and, even earlier, by S. Murata.
 W
WMathematical fiction is a genre of creative fictional work in which mathematics and mathematicians play important roles. The form and the medium of the works are not important. The genre may include poems, short stories, novels or plays; comic books; films, videos, or audios. One of the earliest, and much studied, work of this genre is Flatland: A Romance of Many Dimensions, an 1884 satirical novella by the English schoolmaster Edwin Abbott Abbott. Mathematical fiction may have existed since ancient times, but it was recently rediscovered as a genre of literature; since then there has been a growing body of literature in this genre, and the genre has attracted a growing body of readers. For example, Abbot's Flatland spawned a sequel in the 21st century: a novel titled Flatterland, authored by Ian Stewart and published in 2001.
 W
WIdeas from Mathematics have been used as inspiration for fiber arts including quilt making, knitting, cross-stitch, crochet, embroidery and weaving. A wide range of mathematical concepts have been used as inspiration including topology, graph theory, number theory and algebra. Some techniques such as counted-thread embroidery are naturally geometrical; other kinds of textile provide a ready means for the colorful physical expression of mathematical concepts.
 W
WThe discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability, and the use of paper folds to solve up-to cubic mathematical equations. The discipline is often pursued by the use of washi paper.
 W
WSudoku puzzles can be studied mathematically to answer questions such as "How many filled Sudoku grids are there?", "What is the minimal number of clues in a valid puzzle?" and "In what ways can Sudoku grids be symmetric?" through the use of combinatorics and group theory.
 W
WIn mathematics, the mice problem is a continuous pursuit-evasion problem in which a number of mice are considered to be placed at the corners of a regular polygon. In the classic setup, each then begins to move towards its immediate neighbour. The goal is often to find out at what time the mice meet.
 W
WThe missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it.
 W
WIn mathematics, a Möbius strip, band, or loop, also spelled Mobius or Moebius, is a surface with only one side and only one boundary curve. The Möbius strip is the simplest non-orientable surface. It can be realized as a ruled surface. Its discovery is attributed independently to the German mathematicians Johann Benedict Listing and August Ferdinand Möbius in 1858, though similar structures can be seen in Roman mosaics c. 200–250 AD. Möbius published his results in his articles "Theorie der elementaren Verwandtschaft" (1863) and "Ueber die Bestimmung des Inhaltes eines Polyëders" (1865).
 W
WIn mathematics, the mountain climbing problem is a problem of finding the conditions that two functions forming profiles of a two-dimensional mountain must satisfy, so that two climbers can start on the bottom on the opposite sides of the mountain and coordinate their movements to meet while always staying at the same height. This problem was named and posed in this form by James V. Whittaker (1966), but its history goes back to Tatsuo Homma (1952), who solved a version of it. The problem has been repeatedly rediscovered and solved independently in different context by a number of people.
 W
WIn geometry, the napkin-ring problem involves finding the volume of a "band" of specified height around a sphere, i.e. the part that remains after a hole in the shape of a circular cylinder is drilled through the center of the sphere. It is a counterintuitive fact that this volume does not depend on the original sphere's radius but only on the resulting band's height.
 W
WNim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps or piles. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap or pile. Depending on the version being played, the goal of the game is either to avoid taking the last object or to take the last object.
 W
WPatterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.
 W
WA polyhedron model is a physical construction of a polyhedron, constructed from cardboard, plastic board, wood board or other panel material, or, less commonly, solid material.
 W
WA polyknight is a plane geometric figure formed by selecting cells in a square lattice that could represent the path of a chess knight in which doubling back is allowed. It is a polyform with square cells which are not necessarily connected, comparable to the polyking. Alternatively, it can be interpreted as a connected subset of the vertices of a knight's graph, a graph formed by connecting pairs of lattice squares that are a knight's move apart.
 W
WA polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.
 W
WProjective Set is a real-time card game derived from the older game Set. The deck contains cards consisting of colored dots; some cards are laid out on the table and players attempt to find "Sets" among them. The word projective comes from the game's relation to Projective spaces over the finite field with two elements.
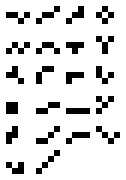 W
WA pseudo-polyomino, also called a polyking, polyplet or hinged polyomino, is a plane geometric figure formed by joining one or more equal squares edge to edge or corner to corner at 90°. It is a polyform with square cells. The polyominoes are a subset of the polykings.
 W
WRithmomachy is a highly complex, early European mathematical board game. The earliest known description of it dates from the eleventh century. A literal translation of the name is "The Battle of the Numbers". The game is much like chess, except most methods of capture depend on the numbers inscribed on each piece.
 W
WSangaku or San Gaku are Japanese geometrical problems or theorems on wooden tablets which were placed as offerings at Shinto shrines or Buddhist temples during the Edo period by members of all social classes.
 W
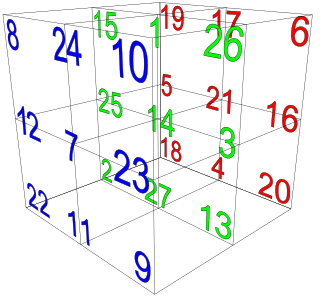
WA simple magic cube is the lowest of six basic classes of magic cube. These classes are based on extra features required.
 W
WThe Slothouber–Graatsma puzzle is a packing problem that calls for packing six 1 × 2 × 2 blocks and three 1 × 1 × 1 blocks into a 3 × 3 × 3 box. The solution to this puzzle is unique. It was named after its inventors Jan Slothouber and William Graatsma.
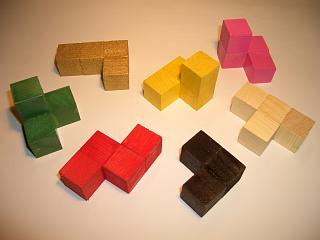 W
WThe Soma cube is a solid dissection puzzle invented by Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg. Its name is alleged to be derived from the fictitious drug soma consumed as a pastime by the establishment in Aldous Huxley's dystopic novel Brave New World.
 W
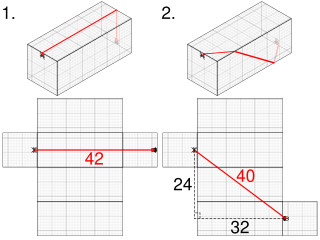
WThe spider and the fly problem is a recreational geodesics problem with an unintuitive solution.
 W
WSquaring the square is the problem of tiling an integral square using only other integral squares. The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares.
 W
WStr8ts is a logic-based number-placement puzzle, invented by Jeff Widderich in 2008. It is distinct from, but shares some properties and rules with Sudoku. The name is derived from the poker straight. The puzzle is published in a number of newspapers internationally, in two book collections, and in downloadable apps. It was featured on the Canadian television show Dragons' Den on November 24, 2010.
 W
WSudoku is a logic-based, combinatorial number-placement puzzle. In classic sudoku, the objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 subgrids that compose the grid contains all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.
 W
WThe tangram is a dissection puzzle consisting of seven flat polygons, called tans, which are put together to form shapes. The objective is to replicate a pattern generally found in a puzzle book using all seven pieces without overlap. Alternatively the tans can be used to create original minimalist designs that are either appreciated for their inherent aesthetic merits or as the basis for challenging others to replicate its outline. It is reputed to have been invented in China sometime around the late 18th century CE and then carried over to America and Europe by trading ships shortly after. It became very popular in Europe for a time, and then again during World War I. It is one of the most widely recognized dissection puzzles in the world and has been used for various purposes including amusement, art, and education.
 W
WTopswops are mathematical problems devised and analysed by the British mathematician John Conway in 1973. Contrary to other games and problems introduced by Conway, these problems have not received much attention from the scientific community. Two famous mathematicians who have contributed to the problem are Martin Gardner and Donald Knuth.
 W
WA two-cube calendar is a desk calendar consisting of two cubes with faces marked by digits 0 through 9. Each face of each cube is marked with a single digit, and it is possible to arrange the cubes so that any chosen day of the month is visible on the two front faces.
 W
WWet-folding is an origami technique developed by Akira Yoshizawa that employs water to dampen the paper so that it can be manipulated more easily. This process adds an element of sculpture to origami, which is otherwise purely geometric. Wet-folding is used very often by professional folders for non-geometric origami, such as animals. Wet-folders usually employ thicker paper than what would usually be used for normal origami, to ensure that the paper does not tear.
 W
WAkira Yoshizawa was a Japanese origamist, considered to be the grandmaster of origami. He is credited with raising origami from a craft to a living art. According to his own estimation made in 1989, he created more than 50,000 models, of which only a few hundred designs were presented as diagrams in his 18 books. Yoshizawa acted as an international cultural ambassador for Japan throughout his career. In 1983, Emperor Hirohito awarded him the Order of the Rising Sun, 5th class, one of the highest honors bestowed in Japan.