 W
WIn information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
 W
WIn mathematics and electronics engineering, a binary Golay code is a type of linear error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics. These codes are named in honor of Marcel J. E. Golay whose 1949 paper introducing them has been called, by E. R. Berlekamp, the "best single published page" in coding theory.
 W
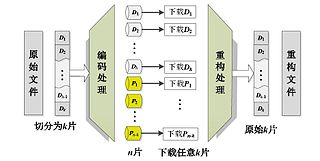
WBinary Reed–Solomon coding (BRS), which belongs to a RS code, is a way of encoding that can fix node data loss in a distributed storage environment. It has maximum distance separable (MDS) encoding properties. Its encoding and decoding rate outperforms conventional RS coding and optimum CRS coding.
 W
WCoding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data.
 W
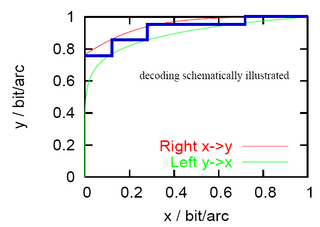
WA detection error tradeoff (DET) graph is a graphical plot of error rates for binary classification systems, plotting the false rejection rate vs. false acceptance rate. The x- and y-axes are scaled non-linearly by their standard normal deviates, yielding tradeoff curves that are more linear than ROC curves, and use most of the image area to highlight the differences of importance in the critical operating region.
 W
WAn extrinsic information transfer chart, commonly called an EXIT chart, is a technique to aid the construction of good iteratively-decoded error-correcting codes.
 W
WIn coding theory, expander codes form a class of error-correcting codes that are constructed from bipartite expander graphs. Along with Justesen codes, expander codes are of particular interest since they have a constant positive rate, a constant positive relative distance, and a constant alphabet size. In fact, the alphabet contains only two elements, so expander codes belong to the class of binary codes. Furthermore, expander codes can be both encoded and decoded in time proportional to the block length of the code.
 W
WThe Hadamard code is an error-correcting code named after Jacques Hadamard that is used for error detection and correction when transmitting messages over very noisy or unreliable channels. In 1971, the code was used to transmit photos of Mars back to Earth from the NASA space probe Mariner 9. Because of its unique mathematical properties, the Hadamard code is not only used by engineers, but also intensely studied in coding theory, mathematics, and theoretical computer science. The Hadamard code is also known under the names Walsh code, Walsh family, and Walsh–Hadamard code in recognition of the American mathematician Joseph Leonard Walsh.
 W
WIn computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect up to two-bit errors or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three. Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.
 W
WIn coding theory, Hamming(7,4) is a linear error-correcting code that encodes four bits of data into seven bits by adding three parity bits. It is a member of a larger family of Hamming codes, but the term Hamming code often refers to this specific code that Richard W. Hamming introduced in 1950. At the time, Hamming worked at Bell Telephone Laboratories and was frustrated with the error-prone punched card reader, which is why he started working on error-correcting codes.
 W
WIn computer science, a hash list is typically a list of hashes of the data blocks in a file or set of files. Lists of hashes are used for many different purposes, such as fast table lookup and distributed databases.
 W
WIn combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column. An example of a 3×3 Latin square is
 W
WIn cryptography and computer science, a hash tree or Merkle tree is a tree in which every leaf node is labelled with the cryptographic hash of a data block, and every non-leaf node is labelled with the cryptographic hash of the labels of its child nodes. Hash trees allow efficient and secure verification of the contents of large data structures. Hash trees are a generalization of hash lists and hash chains.
 W
WThe snake-in-the-box problem in graph theory and computer science deals with finding a certain kind of path along the edges of a hypercube. This path starts at one corner and travels along the edges to as many corners as it can reach. After it gets to a new corner, the previous corner and all of its neighbors must be marked as unusable. The path should never travel to a corner which has been marked unusable.
 W
WIn computing, triple modular redundancy, sometimes called triple-mode redundancy, (TMR) is a fault-tolerant form of N-modular redundancy, in which three systems perform a process and that result is processed by a majority-voting system to produce a single output. If any one of the three systems fails, the other two systems can correct and mask the fault.