 W
WA numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
 W
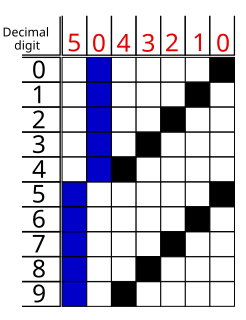
WThe Aiken code is a complementary binary-coded decimal (BCD) code. A group of four bits is assigned to the decimal digits from 0 to 9 according to the following table. The code was developed by Howard Hathaway Aiken and is still used today in digital clocks, pocket calculators and similar devices.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WThe Aiken code is a complementary binary-coded decimal (BCD) code. A group of four bits is assigned to the decimal digits from 0 to 9 according to the following table. The code was developed by Howard Hathaway Aiken and is still used today in digital clocks, pocket calculators and similar devices.
 W
WAlgorism is the technique of performing basic arithmetic by writing numbers in place value form and applying a set of memorized rules and facts to the digits. One who practices algorism is known as an algorist. This positional notation system largely superseded earlier calculation systems that used a different set of symbols for each numerical magnitude, such as Roman numerals, and in some cases required a device such as an abacus.
 W
WAssyro-Chaldean Babylonian cuneiform numerals were written in cuneiform, using a wedge-tipped reed stylus to make a mark on a soft clay tablet which would be exposed in the sun to harden to create a permanent record.
 W
WBi-quinary coded decimal is a numeral encoding scheme used in many abacuses and in some early computers, including the Colossus. The term bi-quinary indicates that the code comprises both a two-state (bi) and a five-state (quinary) component. The encoding resembles that used by many abacuses, with four beads indicating either 0 through 4 or 5 through 9 and another bead indicating which of those ranges.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WA chronogram is a sentence or inscription in which specific letters, interpreted as numerals, stand for a particular date when rearranged. The word, meaning "time writing", derives from the Greek words chronos and gramma.
 W
WNicolas Chuquet was a French mathematician. He invented his own notation for algebraic concepts and exponentiation. He may have been the first mathematician to recognize zero and negative numbers as exponents.
 W
WThe medieval Cistercian numerals, or "ciphers" in nineteenth-century parlance, were developed by the Cistercian monastic order in the early thirteenth century at about the time that Arabic numerals were introduced to northwestern Europe. They are more compact than Arabic or Roman numerals, with a single glyph able to indicate any integer from 1 to 9,999.
 W
WCyrillic numerals are a numeral system derived from the Cyrillic script, developed in the First Bulgarian Empire in the late 10th century. It was used in the First Bulgarian Empire and by South and East Slavic peoples. The system was used in Russia as late as the early 18th century, when Peter the Great replaced it with Arabic numerals as part of his civil script reform initiative. Cyrillic numbers played a role in Peter the Great's currency reform plans, too, with silver wire kopecks issued after 1696 and mechanically minted coins issued between 1700 and 1722 inscribed with the date using Cyrillic numerals. By 1725, Russian Imperial coins had transitioned to Arabic numerals. The Cyrillic numerals may still be found in books written in the Church Slavonic language.
 W
WSeveral genealogical numbering systems have been widely adopted for presenting family trees and pedigree charts in text format. Among the most popular numbering systems are: Ahnentafel, and the Register, NGSQ, Henry, d'Aboville, Meurgey de Tupigny, and de Villiers/Pama Systems.
 W
WGlagolitic numerals are a numeral system derived from the Glagolitic script, generally agreed to have been created in the 9th century by Saint Cyril. They are similar to Cyrillic numerals, except that numeric values are assigned according to the native alphabetic order of the Glagolitic alphabet. Use of Glagolitic script and numerals declined through the Middle Ages and by the 17th century Glagolitic was used almost only in religious writings. It is unclear if the use of Glagolitic numerals persisted as long as the use of Glagolitic script.
 W
WThe Hindu–Arabic numeral system or Indo-Arabic numeral system is a positional decimal numeral system, and is the most common system for the symbolic representation of numbers in the world.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
Wka·ṭa·pa·yā·di system of numerical notation is an ancient Indian alphasyllabic numeral system to depict letters to numerals for easy remembrance of numbers as words or verses. Assigning more than one letter to one numeral and nullifying certain other letters as valueless, this system provides the flexibility in forming meaningful words out of numbers which can be easily remembered.
 W
WThe Kharosthi script, also spelled Kharoshthi or Kharoṣṭhī was an ancient Indian script used by the Khasa, Saka, and Yuezhi peoples, in parts of the Indian subcontinent and present-day eastern Afghanistan. It was used in Central Asia as well. An abugida, it was introduced at least by the middle of the 3rd century BCE, possibly during the 4th century BCE, and remained in use until it died out in its homeland around the 3rd century CE.
 W
WThe Mayan numeral system was the system to represent numbers and calendar dates in the Maya civilization. It was a vigesimal (base-20) positional numeral system. The numerals are made up of three symbols; zero, one and five. For example, thirteen is written as three dots in a horizontal row above two horizontal bars; sometimes it is also written as three vertical dots to the left of two vertical bars. With these three symbols, each of the twenty vigesimal digits could be written.
 W
WMechanical counters are digital counters built using mechanical components. Long before electronics became common, mechanical devices were used to count events. They typically consist of a series of disks mounted on an axle, with the digits zero through nine marked on their edge. The right most disk moves one increment with each event. Each disk except the left-most has a protrusion that, after the completion of one revolution, moves the next disk to the left one increment. Such counters were used as odometers for bicycles and cars and in tape recorders and fuel dispensers and to control manufacturing processes. One of the largest manufacturers was the Veeder-Root company, and their name was often used for this type of counter. Mechanical counters can be made into electromechanical counters, that count electrical impulses, by adding a small solenoid.
 W
WMuisca numerals were the numeric notation system used by the Muisca, one of the civilizations of the Americas before the Spanish conquest of the Muisca. Just like the Mayas, the Muisca had a vigesimal numerical system, based on multiples of twenty. The Muisca numerals were based on counting with fingers and toes. They had specific numbers from one to ten, yet for the numbers between eleven and nineteen they used "foot one" (11) to "foot nine" (19). The number 20 was the 'perfect' number for the Muisca which is visible in their calendar. To calculate higher numbers than 20 they used multiples of their 'perfect' number; gue-muyhica would be "20 times 4", so 80. To describe "50" they used "20 times 2 plus 10"; gue-bosa asaqui ubchihica, transcribed from guêboʒhas aſaqɣ hubchìhicâ. In their calendar, which was lunisolar, they only counted from one to ten and twenty. Each number had a special meaning, related to their deities and certain animals, especially the abundant toads.
 W
WA numerical digit is a single symbol used alone or in combinations, to represent numbers in a positional numeral system. The name "digit" comes from the fact that the ten digits of the hands correspond to the ten symbols of the common base 10 numeral system, i.e. the decimal digits.
 W
WJacques Pelletier du Mans, also spelled Peletier was a humanist, poet and mathematician of the French Renaissance.
 W
WRoman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers in this system are represented by combinations of letters from the Latin alphabet. Modern usage employs seven symbols, each with a fixed integer value:
 W
WThe slashed zero is a representation of the number "0" (zero), with a slash through it. The slashed zero glyph is often used to distinguish the digit "zero" ("0") from the Latin script letter "O" anywhere that the distinction needs emphasis, particularly in encoding systems, scientific and engineering applications, computer programming, and telecommunications. It thus helps to differentiate characters that would otherwise be homoglyphs. It was commonly used during the punched card era, when programs were typically written out by hand, to avoid ambiguity when the character was later typed on a card punch.
 W
WTally marks, also called hash marks, are a unary numeral system. They are a form of numeral used for counting. They are most useful in counting or tallying ongoing results, such as the score in a game or sport, as no intermediate results need to be erased or discarded.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.