25 Search algorithms

In computer science, a search algorithm is any algorithm which solves the search problem, namely, to retrieve information stored within some data structure, or calculated in the search space of a problem domain, either with discrete or continuous values. Specific applications of search algorithms include:Problems in combinatorial optimization, such as: The vehicle routing problem, a form of shortest path problem The knapsack problem: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. The nurse scheduling problem Problems in constraint satisfaction, such as: The map coloring problem Filling in a sudoku or crossword puzzle In game theory and especially combinatorial game theory, choosing the best move to make next Finding a combination or password from the whole set of possibilities Factoring an integer Optimizing an industrial process, such as a chemical reaction, by changing the parameters of the process Retrieving a record from a database Finding the maximum or minimum value in a list or array Checking to see if a given value is present in a set of values

Any-angle path planning algorithms are a subset of pathfinding algorithms that search for a path between two points in space and allow the turns in the path to have any angle. The result is a path that goes directly toward the goal and has relatively few turns. Other pathfinding algorithms such as A* constrain the paths to a grid, which produces jagged, indirect paths.

In backtracking algorithms, backjumping is a technique that reduces search space, therefore increasing efficiency. While backtracking always goes up one level in the search tree when all values for a variable have been tested, backjumping may go up more levels. In this article, a fixed order of evaluation of variables is used, but the same considerations apply to a dynamic order of evaluation.

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root, and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.

Cuckoo hashing is a scheme in computer programming for resolving hash collisions of values of hash functions in a table, with worst-case constant lookup time. The name derives from the behavior of some species of cuckoo, where the cuckoo chick pushes the other eggs or young out of the nest when it hatches; analogously, inserting a new key into a cuckoo hashing table may push an older key to a different location in the table.

In computer science, dancing links is a technique for reverting the operation of deleting a node from a circular doubly linked list. It is particularly useful for efficiently implementing backtracking algorithms, such as Donald Knuth's Algorithm X for the exact cover problem. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem. Some of the better-known exact cover problems include tiling, the n queens problem, and Sudoku.

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking.

In computer science, a dichotomic search is a search algorithm that operates by selecting between two distinct alternatives (dichotomies) at each step. It is a specific type of divide and conquer algorithm. A well-known example is binary search.

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

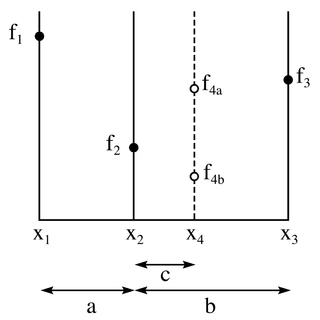
In computer science, a finger search on a data structure is an extension of any search operation that structure supports, where a reference (finger) to an element in the data structure is given along with the query. While the search time for an element is most frequently expressed as a function of the number of elements in a data structure, finger search times are a function of the distance between the element and the finger.

In computer science, finger search trees are a type of binary search tree that keeps pointers to interior nodes, called fingers. The fingers speed up searches, insertions, and deletions for elements close to the fingers, giving amortized O(log n) lookups, and amortized O(1) insertions and deletions. It should not be confused with a finger tree nor a splay tree, although both can be used to implement finger search trees.

In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on biologically inspired operators such as mutation, crossover and selection.

The golden-section search is a technique for finding an extremum of a function inside a specified interval. For a strictly unimodal function with an extremum inside the interval, it will find that extremum, while for an interval containing multiple extrema, it will converge to one of them. If the only extremum on the interval is on a boundary of the interval, it will converge to that boundary point. The method operates by successively narrowing the range of values on the specified interval, which makes it relatively slow, but very robust. The technique derives its name from the fact that the algorithm maintains the function values for four points whose three interval widths are in the ratio 2-φ:2φ-3:2-φ where φ is the golden ratio. These ratios are maintained for each iteration and are maximally efficient. Excepting boundary points, when searching for a minimum, the central point is always less than or equal to the outer points, assuring that a minimum is contained between the outer points. The converse is true when searching for a maximum. The algorithm is the limit of Fibonacci search for many function evaluations. Fibonacci search and golden-section search were discovered by Kiefer (1953).

A hash function is any function that can be used to map data of arbitrary size to fixed-size values. The values returned by a hash function are called hash values, hash codes, digests, or simply hashes. The values are used to index a fixed-size table called a hash table. Use of a hash function to index a hash table is called hashing or scatter storage addressing.

In computing, a hash table is a data structure that implements an associative array abstract data type, a structure that can map keys to values. A hash table uses a hash function to compute an index, also called a hash code, into an array of buckets or slots, from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.

Hopscotch hashing is a scheme in computer programming for resolving hash collisions of values of hash functions in a table using open addressing. It is also well suited for implementing a concurrent hash table. Hopscotch hashing was introduced by Maurice Herlihy, Nir Shavit and Moran Tzafrir in 2008. The name is derived from the sequence of hops that characterize the table's insertion algorithm.

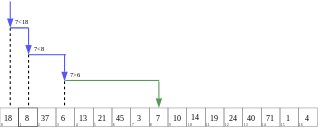
Linear probing is a scheme in computer programming for resolving collisions in hash tables, data structures for maintaining a collection of key–value pairs and looking up the value associated with a given key. It was invented in 1954 by Gene Amdahl, Elaine M. McGraw, and Arthur Samuel and first analyzed in 1963 by Donald Knuth.

In computer science, multiplicative binary search is a variation of binary search that uses a specific permutation of keys in an array instead of the sorted order used by regular binary search. Multiplicative binary search was first described by Thomas Standish in 1980. This algorithm was originally proposed to simplify the midpoint index calculation on small computers without efficient division or shift operations. On modern hardware, the cache-friendly nature of multiplicative binary search makes it suitable for out-of-core search on block-oriented storage as an alternative to B-trees and B+ trees. For optimal performance, the branching factor of a B-tree or B+-tree must match the block size of the file system that it is stored on. The permutation used by multiplicative binary search places the optimal number of keys in the first (root) block, regardless of block size.

In computer science, a perfect hash function for a set S is a hash function that maps distinct elements in S to a set of integers, with no collisions. In mathematical terms, it is an injective function.

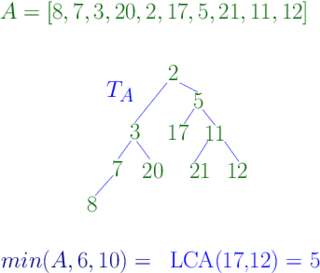
In computer science, a range minimum query (RMQ) solves the problem of finding the minimal value in a sub-array of an array of comparable objects. Range minimum queries have several use cases in computer science, such as the lowest common ancestor problem and the longest common prefix problem (LCP).

A rapidly exploring random tree (RRT) is an algorithm designed to efficiently search nonconvex, high-dimensional spaces by randomly building a space-filling tree. The tree is constructed incrementally from samples drawn randomly from the search space and is inherently biased to grow towards large unsearched areas of the problem. RRTs were developed by Steven M. LaValle and James J. Kuffner Jr. . They easily handle problems with obstacles and differential constraints and have been widely used in autonomous robotic motion planning.

The Siamese method, or De la Loubère method, is a simple method to construct any size of n-odd magic squares. The method was brought to France in 1688 by the French mathematician and diplomat Simon de la Loubère, as he was returning from his 1687 embassy to the kingdom of Siam. The Siamese method makes the creation of magic squares straightforward.

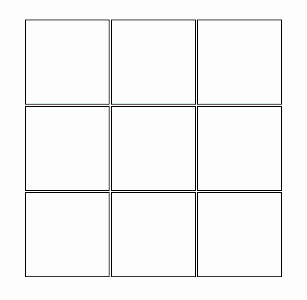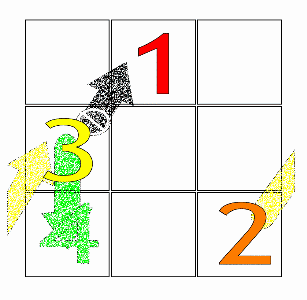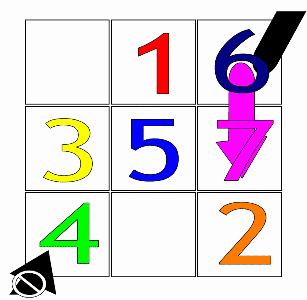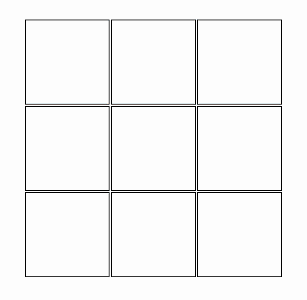
A standard Sudoku contains 81 cells, in a 9×9 grid, and has 9 boxes, each box being the intersection of the first, middle, or last 3 rows, and the first, middle, or last 3 columns. Each cell may contain a number from one to nine, and each number can only occur once in each row, column, and box. A Sudoku starts with some cells containing numbers (clues), and the goal is to solve the remaining cells. Proper Sudokus have one solution. Players and investigators may use a wide range of computer algorithms to solve Sudokus, study their properties, and make new puzzles, including Sudokus with interesting symmetries and other properties.

Yandex Search (Яndex) is a search engine. It is owned by Yandex, based in Russia. In January 2015, Yandex Search generated 51.2% of all of the search traffic in Russia according to LiveInternet.