28 Optimization algorithms and methods

Adaptive coordinate descent is an improvement of the coordinate descent algorithm to non-separable optimization by the use of adaptive encoding. The adaptive coordinate descent approach gradually builds a transformation of the coordinate system such that the new coordinates are as decorrelated as possible with respect to the objective function. The adaptive coordinate descent was shown to be competitive to the state-of-the-art evolutionary algorithms and has the following invariance properties:Invariance with respect to monotonous transformations of the function (scaling) Invariance with respect to orthogonal transformations of the search space (rotation).

In mathematical optimization, affine scaling is an algorithm for solving linear programming problems. Specifically, it is an interior point method, discovered by Soviet mathematician I. I. Dikin in 1967 and reinvented in the U.S. in the mid-1980s.

In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. Artificial ants stand for multi-agent methods inspired by the behavior of real ants. The pheromone-based communication of biological ants is often the predominant paradigm used. Combinations of artificial ants and local search algorithms have become a method of choice for numerous optimization tasks involving some sort of graph, e.g., vehicle routing and internet routing.

In applied mathematics, Basin-hopping is a global optimization technique that iterates by performing random perturbation of coordinates, performing local optimization, and accepting or rejecting new coordinates based on a minimized function value. The algorithm was described in 1997 by David J. Wales and Jonathan Doye. It is a particularly useful algorithm for global optimization in very high-dimensional landscapes, such as finding the minimum energy structure for molecules. Inspired from Monte-Carlo Minimization first suggested by Li and Scheraga.

Column generation or delayed column generation is an efficient algorithm for solving large linear programs.

In mathematical optimization, the criss-cross algorithm is any of a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for linear-fractional programming problems, quadratic-programming problems, and linear complementarity problems.

In mathematical optimization, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed cuts. Such procedures are commonly used to find integer solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory.

Destination dispatch is an optimization technique used for multi-elevator installations, which groups passengers for the same destinations into the same elevators, thereby reducing waiting and travel times when compared to a traditional approach where all passengers wishing to ascend or descend enter any available lift and then request their destination.

Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.

In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.

The Gauss–Newton algorithm is used to solve non-linear least squares problems. It is a modification of Newton's method for finding a minimum of a function. Unlike Newton's method, the Gauss–Newton algorithm can only be used to minimize a sum of squared function values, but it has the advantage that second derivatives, which can be challenging to compute, are not required.

The golden-section search is a technique for finding an extremum of a function inside a specified interval. For a strictly unimodal function with an extremum inside the interval, it will find that extremum, while for an interval containing multiple extrema, it will converge to one of them. If the only extremum on the interval is on a boundary of the interval, it will converge to that boundary point. The method operates by successively narrowing the range of values on the specified interval, which makes it relatively slow, but very robust. The technique derives its name from the fact that the algorithm maintains the function values for four points whose three interval widths are in the ratio 2-φ:2φ-3:2-φ where φ is the golden ratio. These ratios are maintained for each iteration and are maximally efficient. Excepting boundary points, when searching for a minimum, the central point is always less than or equal to the outer points, assuring that a minimum is contained between the outer points. The converse is true when searching for a maximum. The algorithm is the limit of Fibonacci search for many function evaluations. Fibonacci search and golden-section search were discovered by Kiefer (1953).

A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not usually produce an optimal solution, but nonetheless, a greedy heuristic may yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.

The Greedy Triangulation is a method to compute a polygon triangulation or a Point set triangulation using a greedy schema, which adds edges one by one to the solution in strict increasing order by length, with the condition that an edge cannot cut a previously inserted edge.

Interior-point methods are a certain class of algorithms that solve linear and nonlinear convex optimization problems.

Iterated Local Search (ILS) is a term in applied mathematics and computer science defining a modification of local search or hill climbing methods for solving discrete optimization problems.

The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems by minimizing the sum of the squares of the residuals made in the results of every single equation.

Level-set methods (LSM) are a conceptual framework for using level sets as a tool for numerical analysis of surfaces and shapes. The advantage of the level-set model is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects. Also, the level-set method makes it very easy to follow shapes that change topology, for example, when a shape splits in two, develops holes, or the reverse of these operations. All these make the level-set method a great tool for modeling time-varying objects, like inflation of an airbag, or a drop of oil floating in water.

In computer science and electrical engineering, Lloyd's algorithm, also known as Voronoi iteration or relaxation, is an algorithm named after Stuart P. Lloyd for finding evenly spaced sets of points in subsets of Euclidean spaces and partitions of these subsets into well-shaped and uniformly sized convex cells. Like the closely related k-means clustering algorithm, it repeatedly finds the centroid of each set in the partition and then re-partitions the input according to which of these centroids is closest. In this setting, the mean operation is an integral over a region of space, and the nearest centroid operation results in Voronoi diagrams.

In computer science, the maximum sum subarray problem is the task of finding a contiguous subarray with the largest sum, within a given one-dimensional array A[1...n] of numbers. Formally, the task is to find indices and with , such that the sum

Multilevel Coordinate Search (MCS) is an efficient algorithm for bound constrained global optimization using function values only.

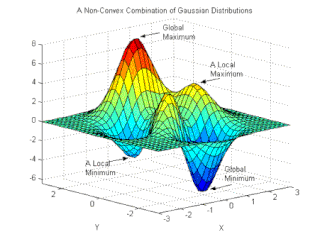
The Nelder–Mead method is a commonly applied numerical method used to find the minimum or maximum of an objective function in a multidimensional space. It is a direct search method and is often applied to nonlinear optimization problems for which derivatives may not be known. However, the Nelder–Mead technique is a heuristic search method that can converge to non-stationary points on problems that can be solved by alternative methods.

ll In calculus, Newton's method is an iterative method for finding the roots of a differentiable function F, which are solutions to the equation F (x) = 0. In optimization, Newton's method is applied to the derivative f ′ of a twice-differentiable function f to find the roots of the derivative, also known as the stationary points of f. These solutions may be minima, maxima, or saddle points.

Pattern search is a family of numerical optimization methods that does not require a gradient. As a result, it can be used on functions that are not continuous or differentiable. One such pattern search method is "convergence", which is based on the theory of positive bases. Optimization attempts to find the best match in a multidimensional analysis space of possibilities.

pSeven is a design space exploration software platform developed by DATADVANCE, extending design, simulation and analysis capabilities and assisting in smarter and faster design decisions. It provides a seamless integration with third party CAD and CAE software tools, powerful multi-objective and robust optimization algorithms, data analysis and uncertainty quantification tools.

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. It is often used when the search space is discrete. For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms such as gradient descent, Branch and Bound.

The spiral optimization (SPO) algorithm is an uncomplicated search concept inspired by spiral phenomena in nature. The first SPO algorithm was proposed for two-dimensional unconstrained optimization based on two-dimensional spiral models. This was extended to n-dimensional problems by generalizing the two-dimensional spiral model to an n-dimensional spiral model. There are effective settings for the SPO algorithm: the periodic descent direction setting and the convergence setting.

Stochastic gradient Langevin dynamics (SGLD), is an optimization technique composed of characteristics from Stochastic gradient descent, a Robbins–Monro optimization algorithm, and Langevin dynamics, a mathematical extension of molecular dynamics models. Like stochastic gradient descent, SGLD is an iterative optimization algorithm which introduces additional noise to the stochastic gradient estimator used in SGD to optimize a differentiable objective function. Unlike traditional SGD, SGLD can be used for Bayesian learning, since the method produces samples from a posterior distribution of parameters based on available data. First described by Welling and Teh in 2011, the method has applications in many contexts which require optimization, and is most notably applied in machine learning problems.