 W
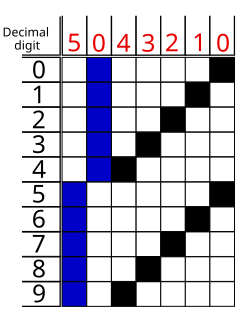
WThe Aiken code is a complementary binary-coded decimal (BCD) code. A group of four bits is assigned to the decimal digits from 0 to 9 according to the following table. The code was developed by Howard Hathaway Aiken and is still used today in digital clocks, pocket calculators and similar devices.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WThe Aiken code is a complementary binary-coded decimal (BCD) code. A group of four bits is assigned to the decimal digits from 0 to 9 according to the following table. The code was developed by Howard Hathaway Aiken and is still used today in digital clocks, pocket calculators and similar devices.
 W
WIn computing, an arithmetic logic unit (ALU) is a combinational digital circuit that performs arithmetic and bitwise operations on integer binary numbers. This is in contrast to a floating-point unit (FPU), which operates on floating point numbers. It is a fundamental building block of many types of computing circuits, including the central processing unit (CPU) of computers, FPUs, and graphics processing units (GPUs).
 W
WIn computer programming, an integer overflow occurs when an arithmetic operation attempts to create a numeric value that is outside of the range that can be represented with a given number of digits – either higher than the maximum or lower than the minimum representable value.
 W
WA barrel shifter is a digital circuit that can shift a data word by a specified number of bits without the use of any sequential logic, only pure combinational logic. One way to implement it is as a sequence of multiplexers where the output of one multiplexer is connected to the input of the next multiplexer in a way that depends on the shift distance. A barrel shifter is often used to shift and rotate n-bits in modern microprocessors, typically within a single clock cycle.
 W
WBi-quinary coded decimal is a numeral encoding scheme used in many abacuses and in some early computers, including the Colossus. The term bi-quinary indicates that the code comprises both a two-state (bi) and a five-state (quinary) component. The encoding resembles that used by many abacuses, with four beads indicating either 0 through 4 or 5 through 9 and another bead indicating which of those ranges.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WThe carry-less product of two binary numbers is the result of carry-less multiplication of these numbers. This operation conceptually works like long multiplication except for the fact that the carry is discarded instead of applied to the more significant position. It can be used to model operations over finite fields, in particular multiplication of polynomials from GF(2)[X], the polynomial ring over GF(2).
 W
WIn combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation. A circular shift is a special kind of cyclic permutation, which in turn is a special kind of permutation. Formally, a circular shift is a permutation σ of the n entries in the tuple such that either modulo n, for all entries i = 1, ..., n
 W
WCORDIC, also known as Volder's algorithm, including Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
 W
WThe Dadda multiplier is a hardware multiplier design invented by computer scientist Luigi Dadda in 1965. It is similar to the Wallace multiplier, but it is slightly faster and requires fewer gates.
 W
WIn mathematics, division by zero is division where the divisor (denominator) is zero. Such a division can be formally expressed as a/0 where a is the dividend (numerator). In ordinary arithmetic, the expression has no meaning, as there is no number which, when multiplied by 0, gives a, and so division by zero is undefined. Since any number multiplied by zero is zero, the expression 0/0 is also undefined; when it is the form of a limit, it is an indeterminate form. Historically, one of the earliest recorded references to the mathematical impossibility of assigning a value to a/0 is contained in George Berkeley's criticism of infinitesimal calculus in 1734 in The Analyst.
 W
WIn computing, floating-point arithmetic (FP) is arithmetic using formulaic representation of real numbers as an approximation to support a trade-off between range and precision. For this reason, floating-point computation is often found in systems which include very small and very large real numbers, which require fast processing times. A number is, in general, represented approximately to a fixed number of significant digits and scaled using an exponent in some fixed base; the base for the scaling is normally two, ten, or sixteen. A number that can be represented exactly is of the following form:
 W
WA floating-point unit is a part of a computer system specially designed to carry out operations on floating-point numbers. Typical operations are addition, subtraction, multiplication, division, and square root. Some FPUs can also perform various transcendental functions such as exponential or trigonometric calculations, but the accuracy can be very low, so that some systems prefer to compute these functions in software.
 W
WGNU Multiple Precision Arithmetic Library (GMP) is a free library for arbitrary-precision arithmetic, operating on signed integers, rational numbers, and floating-point numbers. There are no practical limits to the precision except the ones implied by the available memory (operands may be of up to 232−1 bits on 32-bit machines and 237 bits on 64-bit machines). GMP has a rich set of functions, and the functions have a regular interface. The basic interface is for C, but wrappers exist for other languages, including Ada, C++, C#, Julia, .NET, OCaml, Perl, PHP, Python, R, Ruby and the Wolfram Language. Prior to 2008, Kaffe, a Java virtual machine, used GMP to support Java built-in arbitrary precision arithmetic. Shortly after, GMP support was added to GNU Classpath.
 W
WIn computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect up to two-bit errors or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three. Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.
 W
WIn coding theory, Hamming(7,4) is a linear error-correcting code that encodes four bits of data into seven bits by adding three parity bits. It is a member of a larger family of Hamming codes, but the term Hamming code often refers to this specific code that Richard W. Hamming introduced in 1950. At the time, Hamming worked at Bell Telephone Laboratories and was frustrated with the error-prone punched card reader, which is why he started working on error-correcting codes.
 W
WInterval arithmetic is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods using interval arithmetic can guarantee reliable, mathematically correct results. Instead of representing a value as a single number, interval arithmetic represents each value as a range of possibilities. For example, instead of estimating the height of someone as exactly 2.0 metres, using interval arithmetic one might be certain that that person is somewhere between 1.97 and 2.03 metres.
 W
WInterval arithmetic is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods using interval arithmetic can guarantee reliable, mathematically correct results. Instead of representing a value as a single number, interval arithmetic represents each value as a range of possibilities. For example, instead of estimating the height of someone as exactly 2.0 metres, using interval arithmetic one might be certain that that person is somewhere between 1.97 and 2.03 metres.
 W
WIn computer programming, an integer overflow occurs when an arithmetic operation attempts to create a numeric value that is outside of the range that can be represented with a given number of digits – either higher than the maximum or lower than the minimum representable value.
 W
WInterval arithmetic is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods using interval arithmetic can guarantee reliable, mathematically correct results. Instead of representing a value as a single number, interval arithmetic represents each value as a range of possibilities. For example, instead of estimating the height of someone as exactly 2.0 metres, using interval arithmetic one might be certain that that person is somewhere between 1.97 and 2.03 metres.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.
 W
WIn mathematics and computing, the method of complements is a technique to encode a symmetric range of positive and negative integers in a way that they can use the same algorithm (hardware) for addition throughout the whole range. For a given number of places half of the possible representations of numbers encode the positive numbers, the other half represents their respective additive inverses. The pairs of mutually additive inverse numbers are called complements. Thus subtraction of any number is implemented by adding its complement. Changing the sign of any number is encoded by generating its complement, which can be done by a very simple and efficient algorithm. This method was commonly used in mechanical calculators and is still used in modern computers. The generalized concept of the radix complement is also valuable in number theory, such as in Midy's theorem.
 W
WIn computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another.
 W
WThe GNU Multiple Precision Floating-Point Reliable Library is a GNU portable C library for arbitrary-precision binary floating-point computation with correct rounding, based on GNU Multi-Precision Library.
 W
WMultiple Precision Integers and Rationals (MPIR) is an open-source software multiprecision integer library forked from the GNU Multiple Precision Arithmetic Library (GMP) project. It consists of much code from past GMP releases, and some original contributed code.
 W
WA negative base may be used to construct a non-standard positional numeral system. Like other place-value systems, each position holds multiples of the appropriate power of the system's base; but that base is negative—that is to say, the base b is equal to −r for some natural number r.
 W
WIn software engineering and mathematics, numerical error is the error in the numerical computations.
 W
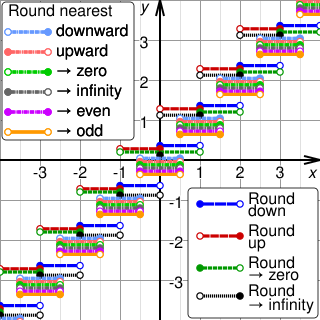
WRounding means replacing a number with an approximate value that has a shorter, simpler, or more explicit representation. For example, replacing $23.4476 with $23.45, the fraction 312/937 with 1/3, or the expression √2 with 1.414.
 W
WA two-out-of-five code is an constant-weight code that provides exactly ten possible combinations of two bits, and is thus used for representing the decimal digits using five bits. Each bit is assigned a weight, such that the set bits sum to the desired value, with an exception for zero.
 W
WA Wallace tree is an efficient hardware implementation of a digital circuit that multiplies two integers. It was devised by the Australian computer scientist Chris Wallace in 1964.
 W
WIn computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.