42 Trees (data structures)

In computer science, a tree is a widely used abstract data type that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.

In computer science, an abstract syntax tree (AST), or just syntax tree, is a tree representation of the abstract syntactic structure of source code written in a programming language. Each node of the tree denotes a construct occurring in the source code.

An anatree is a data structure designed to solve anagrams. Solving an anagram is the problem of finding a word from a given list of letters. These problems are commonly encountered in word games like Scrabble or in newspaper crossword puzzles. The problem for the wordwheel also has the condition that the central letter appear in all the words framed with the given set. Some other conditions may be introduced regarding the frequency of each of the letters in the given input string. These problems are classified as Constraint satisfaction problem in computer science literature.

In computing, tree data structures, and game theory, the branching factor is the number of children at each node, the outdegree. If this value is not uniform, an average branching factor can be calculated.

In number theory, the Calkin–Wilf tree is a tree in which the vertices correspond one-to-one to the positive rational numbers. The tree is rooted at the number 1, and any rational number expressed in simplest terms as the fraction a/b has as its two children the numbers a/a + b and a + b/b. Every positive rational number appears exactly once in the tree.

A dendrogram is a diagram representing a tree. This diagrammatic representation is frequently used in different contexts:in hierarchical clustering, it illustrates the arrangement of the clusters produced by the corresponding analyses. in computational biology, it shows the clustering of genes or samples, sometimes in the margins of heatmaps. in phylogenetics, it displays the evolutionary relationships among various biological taxa. In this case, the dendrogram is also called a phylogenetic tree.

A dialogue tree, or conversation tree, is a gameplay mechanic that is used throughout many adventure games and role-playing video games. When interacting with a non-player character, the player is given a choice of what to say and makes subsequent choices until the conversation ends. Certain video game genres, such as visual novels and dating sims, revolve almost entirely around these character interactions and branching dialogues.

In computer science a doubly logarithmic tree is a tree where each internal node of height 1, the tree layer above the leaves, has two children, and each internal node of height has children. Each child of the root contains leaves. The number of children at a node as we go from leaf to root is 0,2,2,4,16, 256, 65536, ...

Dynamic Syntax Tree (DST), was created by M.Barzanti as an alternative of Abstract syntax tree and Parse tree representation of the structure of source code written in a programming language. Unlike the Statically typed programming languages, the analysis of a Dynamic programming language has to estimate the Type system from the code fragment semantics, as well as all Configuration files and Binary files. Dynamic Syntax Tree implementation also take into account non-static and non-typed implicit and explicit Declaration s, so that the resulting information covers most of readable dynamic code fragments.

A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.

The "figurative system of human knowledge", sometimes known as the tree of Diderot and d'Alembert, was a tree developed to represent the structure of knowledge itself, produced for the Encyclopédie by Jean le Rond d'Alembert and Denis Diderot.

In computer science, finger search trees are a type of binary search tree that keeps pointers to interior nodes, called fingers. The fingers speed up searches, insertions, and deletions for elements close to the fingers, giving amortized O(log n) lookups, and amortized O(1) insertions and deletions. It should not be confused with a finger tree nor a splay tree, although both can be used to implement finger search trees.

In computer science, a generalized suffix tree is a suffix tree for a set of strings. Given the set of strings of total length , it is a Patricia tree containing all suffixes of the strings. It is mostly used in bioinformatics.

In fractal geometry, the H tree, or T-branching, is a fractal tree structure constructed from perpendicular line segments, each smaller by a factor of the square root of 2 from the next larger adjacent segment. It is so called because its repeating pattern resembles the letter "H". It has Hausdorff dimension 2, and comes arbitrarily close to every point in a rectangle. Its applications include VLSI design and microwave engineering.

A hyperbolic tree is an information visualization and graph drawing method inspired by hyperbolic geometry.

An implicit k-d tree is a k-d tree defined implicitly above a rectilinear grid. Its split planes' positions and orientations are not given explicitly but implicitly by some recursive splitting-function defined on the hyperrectangles belonging to the tree's nodes. Each inner node's split plane is positioned on a grid plane of the underlying grid, partitioning the node's grid into two subgrids.

In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key. k-d trees are a special case of binary space partitioning trees.

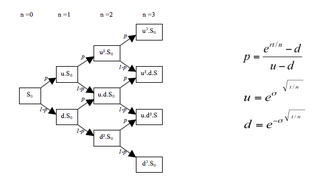
In finance, a lattice model is a technique applied to the valuation of derivatives, where a discrete time model is required. For equity options, a typical example would be pricing an American option, where a decision as to option exercise is required at "all" times before and including maturity. A continuous model, on the other hand, such as Black–Scholes, would only allow for the valuation of European options, where exercise is on the option's maturity date. For interest rate derivatives lattices are additionally useful in that they address many of the issues encountered with continuous models, such as pull to par. The method is also used for valuing certain exotic options, where because of path dependence in the payoff, Monte Carlo methods for option pricing fail to account for optimal decisions to terminate the derivative by early exercise, though methods now exist for solving this problem.

In computer science, the log-structured merge-tree is a data structure with performance characteristics that make it attractive for providing indexed access to files with high insert volume, such as transactional log data. LSM trees, like other search trees, maintain key-value pairs. LSM trees maintain data in two or more separate structures, each of which is optimized for its respective underlying storage medium; data is synchronized between the two structures efficiently, in batches.

In graph theory, an m-ary tree is a rooted tree in which each node has no more than m children. A binary tree is the special case where m = 2, and a ternary tree is another case with m = 3 that limits its children to three.

In cryptography and computer science, a hash tree or Merkle tree is a tree in which every leaf node is labelled with the cryptographic hash of a data block, and every non-leaf node is labelled with the cryptographic hash of the labels of its child nodes. Hash trees allow efficient and secure verification of the contents of large data structures. Hash trees are a generalization of hash lists and hash chains.

An octree is a tree data structure in which each internal node has exactly eight children. Octrees are most often used to partition a three-dimensional space by recursively subdividing it into eight octants. Octrees are the three-dimensional analog of quadtrees. The name is formed from oct + tree, but note that it is normally written "octree" with only one "t". Octrees are often used in 3D graphics and 3D game engines.

In computer science, an in-tree or parent pointer tree is an N-ary tree data structure in which each node has a pointer to its parent node, but no pointers to child nodes. When used to implement a set of stacks, the structure is called a spaghetti stack, cactus stack or saguaro stack. Parent pointer trees are also used as disjoint-set data structures.

A parse tree or parsing tree or derivation tree or concrete syntax tree is an ordered, rooted tree that represents the syntactic structure of a string according to some context-free grammar. The term parse tree itself is used primarily in computational linguistics; in theoretical syntax, the term syntax tree is more common.

A phylogenetic tree or evolutionary tree is a branching diagram or "tree" showing the evolutionary relationships among various biological species or other entities—their phylogeny —based upon similarities and differences in their physical or genetic characteristics. All life on Earth is part of a single phylogenetic tree, indicating common ancestry.

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information".

A radial tree, or radial map, is a method of displaying a tree structure in a way that expands outwards, radially. It is one of many ways to visually display a tree, with examples extending back to the early 20th century. In use, it is a type of information graphic.

In computer science, a radix tree is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at most the radix r of the radix tree, where r is a positive integer and a power x of 2, having x ≥ 1. Unlike regular trees, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets and for sets of strings that share long prefixes.

In computer science, a self-balancing binary search tree is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions.

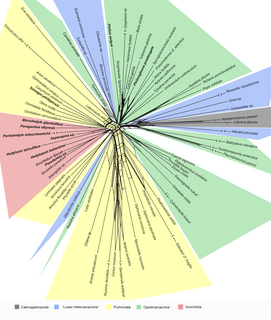
A split in phylogenetics is a bipartition of a set of taxa, and the smallest unit of information in unrooted phylogenetic trees: each edge of an unrooted phylogenetic tree represents one split, and the tree can be efficiently reconstructed from its set of splits. Moreover, when given several trees, the splits occurring in more than half of these trees give rise to a consensus tree, and the splits occurring in a smaller fraction of the trees generally give rise to a consensus Split Network.

In graph theory, a branch of mathematics, the triconnected components of a biconnected graph are a system of smaller graphs that describe all of the 2-vertex cuts in the graph. An SPQR tree is a tree data structure used in computer science, and more specifically graph algorithms, to represent the triconnected components of a graph. The SPQR tree of a graph may be constructed in linear time and has several applications in dynamic graph algorithms and graph drawing.

In number theory, the Stern–Brocot tree is an infinite complete binary tree in which the vertices correspond one-for-one to the positive rational numbers, whose values are ordered from the left to the right as in a search tree.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.

In computer science, a ternary tree is a tree data structure in which each node has at most three child nodes, usually distinguished as "left", “mid” and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to the "root" node, if it exists. Any node in the data structure can be reached by starting at root node and repeatedly following references to either the left, mid or right child.

In automata theory, a tree is a particular way of representing a tree structure as sequences of natural numbers.

A tree network, or star-bus network, is a hybrid network topology in which star networks are interconnected via bus networks. Tree networks are hierarchical, and each node can have an arbitrary number of child nodes.

In mathematics, a tree of primitive Pythagorean triples is a data tree in which each node branches to three subsequent nodes with the infinite set of all nodes giving all primitive Pythagorean triples without duplication.

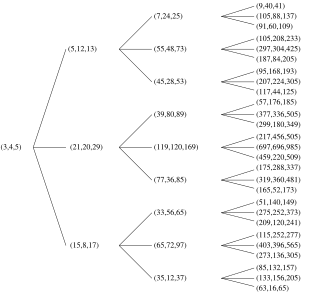
A tree structure or tree diagram is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to a biological tree, with the "stem" at the top and the "leaves" at the bottom.

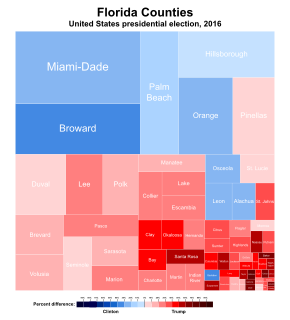
In information visualization and computing, treemapping is a method for displaying hierarchical data using nested figures, usually rectangles.

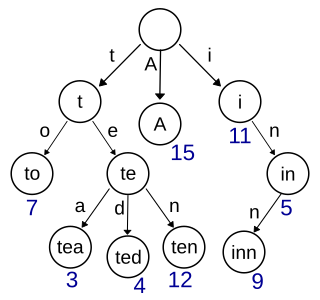
In computer science, a trie, also called digital tree or prefix tree, is a kind of search tree—an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated; i.e., the value of the key is distributed across the structure. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Keys tend to be associated with leaves, though some inner nodes may correspond to keys of interest. Hence, keys are not necessarily associated with every node. For the space-optimized presentation of prefix tree, see compact prefix tree.

The Wavelet Tree is a succinct data structure to store strings in compressed space. It generalizes the and operations defined on bitvectors to arbitrary alphabets.