 W
WIn computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics.
 W
WIn graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs.
 W
WAn and-inverter graph (AIG) is a directed, acyclic graph that represents a structural implementation of the logical functionality of a circuit or network. An AIG consists of two-input nodes representing logical conjunction, terminal nodes labeled with variable names, and edges optionally containing markers indicating logical negation. This representation of a logic function is rarely structurally efficient for large circuits, but is an efficient representation for manipulation of boolean functions. Typically, the abstract graph is represented as a data structure in software.
 W
WA call graph is a control flow graph, which represents calling relationships between subroutines in a computer program. Each node represents a procedure and each edge (f, g) indicates that procedure f calls procedure g. Thus, a cycle in the graph indicates recursive procedure calls.
 W
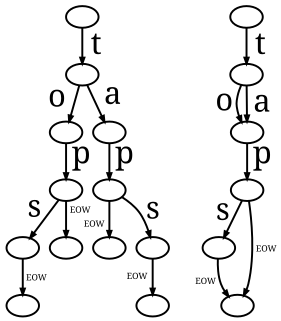
WIn computer science, a deterministic acyclic finite state automaton (DAFSA), also called a directed acyclic word graph is a data structure that represents a set of strings, and allows for a query operation that tests whether a given string belongs to the set in time proportional to its length. Algorithms exist to construct and maintain such automata, while keeping them minimal.
 W
WIn computer science, a graph-structured stack (GSS) is a directed acyclic graph where each directed path represents a stack. The graph-structured stack is an essential part of Tomita's algorithm, where it replaces the usual stack of a pushdown automaton. This allows the algorithm to encode the nondeterministic choices in parsing an ambiguous grammar, sometimes with greater efficiency.
 W
WA node is a basic unit of a data structure, such as a linked list or tree data structure. Nodes contain data and also may link to other nodes. Links between nodes are often implemented by pointers.
 W
WA scene graph is a general data structure commonly used by vector-based graphics editing applications and modern computer games, which arranges the logical and often spatial representation of a graphical scene. It is a collection of nodes in a graph or tree structure. A tree node may have many children but only a single parent, with the effect of a parent applied to all its child nodes; an operation performed on a group automatically propagates its effect to all of its members. In many programs, associating a geometrical transformation matrix at each group level and concatenating such matrices together is an efficient and natural way to process such operations. A common feature, for instance, is the ability to group related shapes and objects into a compound object that can then be manipulated as easily as a single object.
 W
WIn graph theory, a branch of mathematics, the triconnected components of a biconnected graph are a system of smaller graphs that describe all of the 2-vertex cuts in the graph. An SPQR tree is a tree data structure used in computer science, and more specifically graph algorithms, to represent the triconnected components of a graph. The SPQR tree of a graph may be constructed in linear time and has several applications in dynamic graph algorithms and graph drawing.