21 Euclidean symmetries

In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space ; that is, the transformations of that space that preserve the Euclidean distance between any two points. The group depends only on the dimension n of the space, and is commonly denoted E(n) or ISO(n).

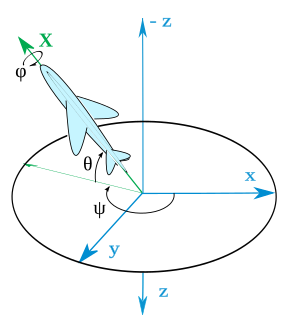
In ballistics and flight dynamics, axes conventions are standardized ways of establishing the location and orientation of coordinate axes for use as a frame of reference. Mobile objects are normally tracked from an external frame considered fixed. Other frames can be defined on those mobile objects to deal with relative positions for other objects. Finally, attitudes or orientations can be described by a relationship between the external frame and the one defined over the mobile object.

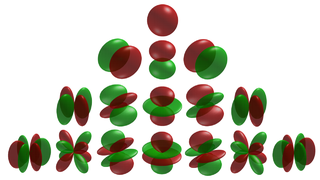
In fields like computational chemistry and solid-state and condensed matter physics the so-called atomic orbitals, or spin-orbitals, as they appear in textbooks on quantum physics, are often partially replaced by cubic harmonics for a number of reasons. These harmonics are usually named tesseral harmonics in the field of condensed matter physics in which the name 'Kubic harmonics' rather refers to the irreducible representations in the Cubic point-group.

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.

In plane geometry the Estermann measure is a number defined for any bounded convex set describing how close to being centrally symmetric it is. It is the ratio of areas between the given set and its smallest centrally symmetric convex superset. It is one for a set that is centrally symmetric, and less than one for sets whose closure is not centrally symmetric. It is invariant under affine transformations of the plane.

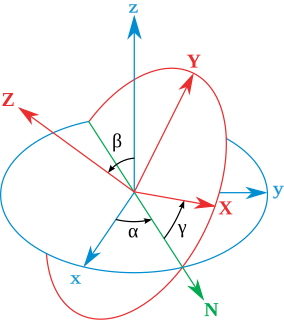
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.

In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two rotations is also a rotation. Therefore the set of rotations has a group structure, known as a rotation group.

In mathematics, a frieze or frieze pattern is a design on a two-dimensional surface that is repetitive in one direction. Such patterns occur frequently in architecture and decorative art. A frieze group is the set of symmetries of a frieze pattern, specifically the set of isometries of the pattern, that is geometric transformations built from rigid motions and reflections that preserve the pattern. The mathematical study of frieze patterns reveals that they can be classified into seven types according to their symmetries.

In 2-dimensional geometry, a glide reflection is a symmetry operation that consists of a reflection over a line and then translation along that line, combined into a single operation. The intermediate step between reflection and translation can look different from the starting configuration, so objects with glide symmetry are in general, not symmetrical under reflection alone. In group theory, the glide plane is classified as a type of opposite isometry of the Euclidean plane

In plane geometry the Kovner–Besicovitch measure is a number defined for any bounded convex set describing how close to being centrally symmetric it is. It is the fraction of the area of the set that can be covered by its largest centrally symmetric subset.

In mathematics, the orthogonal group in dimension n, denoted O(n), is the group of distance-preserving transformations of a Euclidean space of dimension n that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of n×n orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.

In geometry, a point group is a group of geometric symmetries (isometries) that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O(d). Point groups can be realized as sets of orthogonal matrices M that transform point x into point y:y = Mx

In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group, U(1), a group also known as the circle group.

In geometry, a point reflection or inversion in a point is a type of isometry of Euclidean space. An object that is invariant under a point reflection is said to possess point symmetry; if it is invariant under point reflection through its center, it is said to possess central symmetry or to be centrally symmetric.

In statistics, Procrustes analysis is a form of statistical shape analysis used to analyse the distribution of a set of shapes. The name Procrustes refers to a bandit from Greek mythology who made his victims fit his bed either by stretching their limbs or cutting them off.

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis would look like q. Its image by reflection in a horizontal axis would look like b. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state.

Reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry, is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space. A clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude.

Rotation around a fixed axis is a special case of rotational motion. The fixed-axis hypothesis excludes the possibility of an axis changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will appear.

In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure or a space by the same distance in a given direction. A translation can also be interpreted as the addition of a constant vector to every point, or as shifting the origin of the coordinate system. In a Euclidean space, any translation is an isometry.

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles and tiles as well as wallpaper.