 W
WActuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.
 W
WAddition is one of the four basic operations of arithmetic, the other three being subtraction, multiplication and division. The addition of two whole numbers results in the total amount or sum of those values combined. The example in the adjacent image shows a combination of three apples and two apples, making a total of five apples. This observation is equivalent to the mathematical expression "3 + 2 = 5".
 W
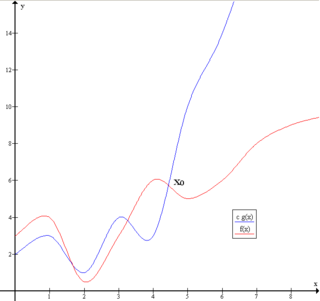
WAmbiguity is a type of meaning in which a phrase, statement or resolution is not explicitly defined, making several interpretations plausible. A common aspect of ambiguity is uncertainty. It is thus an attribute of any idea or statement whose intended meaning cannot be definitively resolved according to a rule or process with a finite number of steps.
 W
WBig O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation.
 W
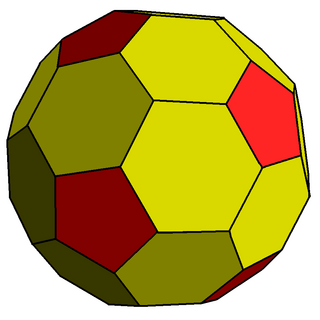
WIn geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.
 W
WThe chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (geometry) (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.
 W
WIn geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
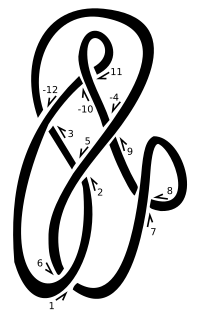 W
WIn the mathematical field of knot theory, the Dowker–Thistlethwaite (DT) notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and Morwen Thistlethwaite, who refined a notation originally due to Peter Guthrie Tait.
 W
WIn mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or .
 W
WIn science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a chemical formula. The informal use of the term formula in science refers to the general construct of a relationship between given quantities.
 W
WA formula calculator is a software calculator that can perform a calculation in two steps:Enter the calculation by typing it in from the keyboard. Press a single button or key to see the final result.
 W
WBig O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation.
 W
WIn queueing theory, a discipline within the mathematical theory of probability, Kendall's notation is the standard system used to describe and classify a queueing node. D. G. Kendall proposed describing queueing models using three factors written A/S/c in 1953 where A denotes the time between arrivals to the queue, S the service time distribution and c the number of service channels open at the node. It has since been extended to A/S/c/K/N/D where K is the capacity of the queue, N is the size of the population of jobs to be served, and D is the queueing discipline.
 W
WIn calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively.
 W
WMultiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction and division. The result of a multiplication operation is called a product.
 W
WMusic notation or musical notation is any system used to visually represent aurally perceived music played with instruments or sung by the human voice through the use of written, printed, or otherwise-produced symbols, including notation for durations of absence of sound such as rests.
 W
WThe Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
 W
WA numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
 W
WIn mathematics and physics, Penrose graphical notation or tensor diagram notation is a visual depiction of multilinear functions or tensors proposed by Roger Penrose in 1971. A diagram in the notation consists of several shapes linked together by lines. The notation has been studied extensively by Predrag Cvitanović, who used it to classify the classical Lie groups. It has also been generalized using representation theory to spin networks in physics, and with the presence of matrix groups to trace diagrams in linear algebra. The notation widely appears in modern quantum theory, particularly in matrix product states and quantum circuits.
 W
WPositional notation denotes usually the extension to any base of the Hindu–Arabic numeral system. More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred. In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string.
 W
WQuipu are recording devices fashioned from strings historically used by a number of cultures in the region of Andean South America. Knotted strings were used by many other cultures such as the ancient Chinese and native Hawaiians, but such practices should not be confused with the quipu, which refers only to the Andean device.
 W
WIn geometry, the Schläfli symbol is a notation of the form {p,q,r,...} that defines regular polytopes and tessellations.
 W
WA software calculator is a calculator that has been implemented as a computer program, rather than as a physical hardware device.
 W
WTally marks, also called hash marks, are a unary numeral system. They are a form of numeral used for counting. They are most useful in counting or tallying ongoing results, such as the score in a game or sport, as no intermediate results need to be erased or discarded.
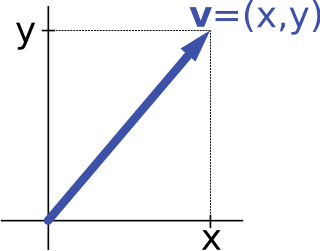 W
WVector notation is a commonly used mathematical notation for working with mathematical vectors, which may be geometric vectors or members of vector spaces.
 W
WIn geometry, a vertex configuration is a shorthand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron.
 W
WIn geometry, the Wythoff symbol is a notation representing a Wythoff construction of a uniform polyhedron or plane tiling within a Schwarz triangle. It was first used by Coxeter, Longuet-Higgins and Miller in their enumeration of the uniform polyhedra. Later the Coxeter diagram was developed to mark uniform polytopes and honeycombs in n-dimensional space within a fundamental simplex.
 W
WZenzizenzizenzic is an obsolete form of mathematical notation representing the eighth power of a number, dating from a time when powers were written out in words rather than as superscript numbers. This term was suggested by Robert Recorde, a 16th-century Welsh writer of popular mathematics textbooks, in his 1557 work The Whetstone of Witte ; he wrote that it "doeth represent the square of squares squaredly".