 W
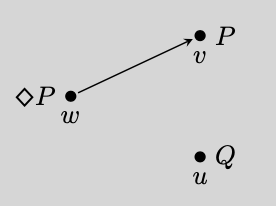
WAn accessibility relation is a relation which plays a key role in assigning truth values to sentences in the relational semantics for modal logic. In relational semantics, a modal formula's truth value at a possible world can depend on what's true at another possible world , but only if the accessibility relation relates to . For instance, if holds at some world such that , the formula will be true at . The fact is crucial. If did not relate to , then would be false at unless also held at some other world such that .
 W
WIn mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.
 W
WIn mathematics, any two elements x and y of a set P that is partially ordered by a binary relation ≤ are comparable when either x ≤ y or y ≤ x. If it is not the case that x and y are comparable, then they are called incomparable.
 W
WIn mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours. The covering relation is commonly used to graphically express the partial order by means of the Hasse diagram.
 W
WIn mathematics, when the elements of some set S have a notion of equivalence defined on them, then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent.
 W
WIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word partial in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable.
 W
WThe mathematical notion of quasitransitivity is a weakened version of transitivity that is used in social choice theory and microeconomics. Informally, a relation is quasitransitive if it is symmetric for some values and transitive elsewhere. The concept was introduced by Sen (1969) to study the consequences of Arrow's theorem.
 W
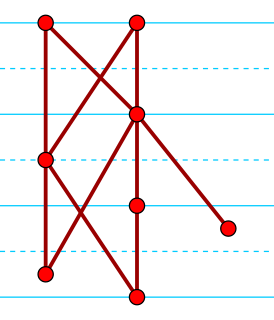
WIn order theory, a branch of mathematics, a semiorder is a type of ordering for items with numerical scores, where items with widely differing scores are compared by their scores and where scores within a given margin of error are deemed incomparable. Semiorders were introduced and applied in mathematical psychology by Duncan Luce (1956) as a model of human preference. They generalize strict weak orderings, in which items with equal scores may be tied but there is no margin of error. They are a special case of partial orders and of interval orders, and can be characterized among the partial orders by additional axioms, or by two forbidden four-item suborders.
 W
WIn order-theoretic mathematics, a series-parallel partial order is a partially ordered set built up from smaller series-parallel partial orders by two simple composition operations.
 W
WIn mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set, some of whose members may be tied with each other. Weak orders are a generalization of totally ordered sets and are in turn generalized by partially ordered sets and preorders.