 W
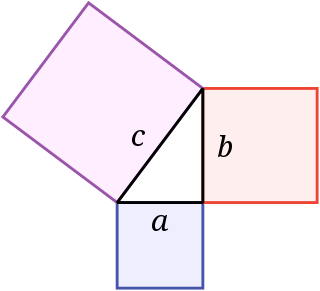
WIn mathematics, the Pythagorean theorem, or Pythagoras's theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the Pythagorean equation:
 W
WThe alpha max plus beta min algorithm is a high-speed approximation of the square root of the sum of two squares. The square root of the sum of two squares, also known as Pythagorean addition, is a useful function, because it finds the hypotenuse of a right triangle given the two side lengths, the norm of a 2-D vector, or the magnitude of a complex number z = a + bi given the real and imaginary parts.
 W
WIn Euclidean geometry, the British flag theorem says that if a point P is chosen inside rectangle ABCD then the sum of the squares of the Euclidean distances from P to two opposite corners of the rectangle equals the sum to the other two opposite corners. As an equation:
 W
WIn mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century.
 W
WIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c satisfy the equation an + bn = cn for any integer value of n greater than 2. The cases n = 1 and n = 2 have been known since antiquity to have infinitely many solutions.
 W
WIn geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. For example, if one of the other sides has a length of 3 and the other has a length of 4, then their squares add up to 25. The length of the hypotenuse is the square root of 25, that is, 5.
 W
WA Pythagorean quadruple is a tuple of integers a, b, c and d, such that a2 + b2 + c2 = d2. They are solutions of a Diophantine equation and often only positive integer values are considered. However, to provide a more complete geometric interpretation, the integer values can be allowed to be negative and zero with the only condition being that d > 0. In this setting, a Pythagorean quadruple (a, b, c, d) defines a cuboid with integer side lengths |a|, |b|, and |c|, whose space diagonal has integer length d; with this interpretation, Pythagorean quadruples are thus also called Pythagorean boxes. In this article we will assume, unless otherwise stated, that the values of a Pythagorean quadruple are all positive integers.
 W
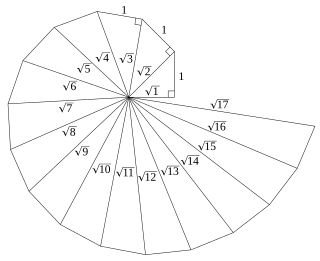
WIn geometry, the spiral of Theodorus is a spiral composed of right triangles, placed edge-to-edge. It was named after Theodorus of Cyrene.
 W
WThe square root of 2, or the one-half power of 2, written in mathematics as or , is the positive algebraic number that, when multiplied by itself, equals the number 2. Technically, it must be called the principal square root of 2, to distinguish it from the negative number with the same property.
 W
WA Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.