 W
WRobin K. Bullough was a British mathematical physicist known for his contributions to the theory of solitons, in particular for his role in the development of the theory of the optical soliton, now commonly used, for example, in the theory of trans-oceanic optical fibre communication theory, but first recognised in Bullough's work on ultra-short optical pulses. He is also known for deriving exact solutions to the nonlinear equations describing these solitons and for associated work on integrable systems, infinite-dimensional Hamiltonian systems, and the statistical mechanics for these systems. Bullough also contributed to nonlinear mathematical physics, including Bose–Einstein condensation in magnetic traps.
 W
WIn fluid dynamics, the Camassa–Holm equation is the integrable, dimensionless and non-linear partial differential equation
 W
WIn string theory, a domain wall is a theoretical (d−1)-dimensional singularity. A domain wall is meant to represent an object of codimension one embedded into space. For example, D8-branes are domain walls in type II string theory. In M-theory, the existence of Horava–Witten domain walls, "ends of the world" that carry an E8 gauge theory, is important for various relations between superstring theory and M-theory.
 W
WIn mathematics and physics, the Kadomtsev–Petviashvili equation is a partial differential equation to describe nonlinear wave motion. Named after Boris Borisovich Kadomtsev and Vladimir Iosifovich Petviashvili, the KP equation is usually written as:
 W
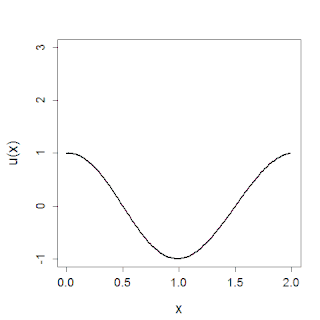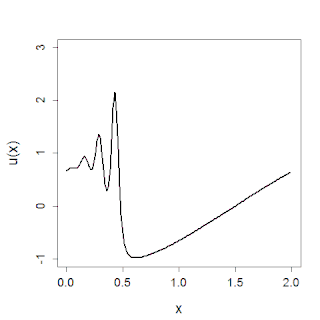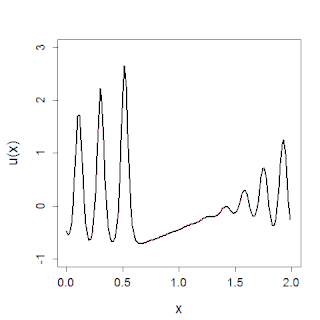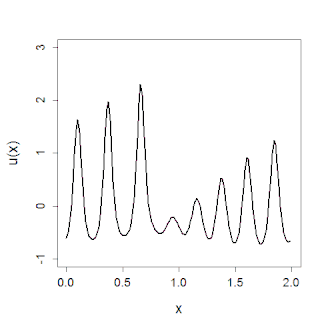
WIn mathematics, the Korteweg–de Vries (KdV) equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified. KdV can be solved by means of the inverse scattering transform. The mathematical theory behind the KdV equation is a topic of active research. The KdV equation was first introduced by Boussinesq and rediscovered by Diederik Korteweg and Gustav de Vries (1895).
 W
WIn mathematics, a loop group is a group of loops in a topological group G with multiplication defined pointwise.
 W
WIn mathematics and physics, a nonlinear partial differential equation is a partial differential equation with nonlinear terms. They describe many different physical systems, ranging from gravitation to fluid dynamics, and have been used in mathematics to solve problems such as the Poincaré conjecture and the Calabi conjecture. They are difficult to study: there are almost no general techniques that work for all such equations, and usually each individual equation has to be studied as a separate problem.
 W
WThe Peregrine soliton is an analytic solution of the nonlinear Schrödinger equation. This solution was proposed in 1983 by Howell Peregrine, researcher at the mathematics department of the University of Bristol.
 W
WIn optics, a nematicon is a spatial soliton in nematic liquid crystals (NLC). The name was invented in 2003 by G. Assanto. and used thereafter Nematicons are generated by a special type of optical nonlinearity present in NLC: the light induced reorientation of the molecular director. This nonlinearity arises from the fact that the molecular director tends to align along the electric field of light. Nematicons are easy to generate because the NLC dielectric medium exhibits the following properties:A very large nonlinear response : the effective nonlinearity is typically eight orders of magnitude larger than that of carbon disulfide. This means that much lower optical powers are necessary to obtain the same refractive index variation (increase) or self-focusing to balance out diffraction. A nonlocal response : the nonlinear response is not limited to the location of the optical field. Instead the response profile is wider than the light beam. A high nonlocality allows for stable soliton propagation even in the case of two transverse dimensions. Higher or lower powers than the exact value required for a soliton to exist lead to breathing solitons.
 W
WIn mathematics and physics, a soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium. Solitons are the solutions of a widespread class of weakly nonlinear dispersive partial differential equations describing physical systems.