 W
WAnne's theorem, named after the French mathematician Pierre-Leon Anne (1806–1850), is a statement from Euclidean geometry, which describes an equality of certain areas within a convex quadrilateral.
 W
WIn geometry, Bretschneider's formula is the following expression for the area of a general quadrilateral:
 W
WIn Euclidean geometry, the British flag theorem says that if a point P is chosen inside rectangle ABCD then the sum of the squares of the Euclidean distances from P to two opposite corners of the rectangle equals the sum to the other two opposite corners. As an equation:
 W
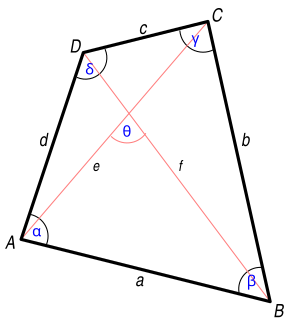
WEuler's quadrilateral theorem or Euler's law on quadrilaterals, named after Leonhard Euler (1707–1783), describes a relation between the sides of a convex quadrilateral and its diagonals. It is a generalisation of the parallelogram law which in turn can be seen as generalisation of the Pythagorean theorem. Because of the latter the restatement of the Pythagorean theorem in terms of quadrilaterals is occasionally called the Euler–Pythagoras theorem.
 W
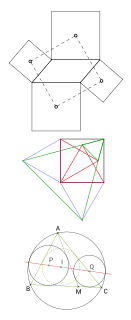
WThe Finsler–Hadwiger theorem is statement in Euclidean plane geometry that describes a third square derived from any two squares that share a vertex. The theorem is named after Paul Finsler and Hugo Hadwiger, who published it in 1937 as part of the same paper in which they published the Hadwiger–Finsler inequality relating the side lengths and area of a triangle.
 W
WIn mathematics, the simplest form of the parallelogram law belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals. Using the notation in the diagram on the right, the sides are (AB), (BC), (CD), (DA). But since in Euclidean geometry a parallelogram necessarily has opposite sides equal, i.e. (AB) = (CD) and (BC) = (DA), the law can be stated as
 W
WThébault's theorem is the name given variously to one of the geometry problems proposed by the French mathematician Victor Thébault, individually known as Thébault's problem I, II, and III.
 W
WThe theorem of the gnomon states that certain parallelograms occurring in a gnomon have areas of equal size.
 W
WIn plane geometry, Van Aubel's theorem describes a relationship between squares constructed on the sides of a quadrilateral. Starting with a given convex quadrilateral, construct a square, external to the quadrilateral, on each side. Van Aubel's theorem states that the two line segments between the centers of opposite squares are of equal lengths and are at right angles to one another. Another way of saying the same thing is that the center points of the four squares form the vertices of an equidiagonal orthodiagonal quadrilateral. The theorem is named after H. H. van Aubel, who published it in 1878.
 W
WVarignon's theorem is a statement in Euclidean geometry, that deals with the construction of a particular parallelogram, the Varignon parallelogram, from an arbitrary quadrilateral (quadrangle). It is named after Pierre Varignon, whose proof was published posthumously in 1731.