10 Theory of probability distributions

Benford's law, also called the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation about the frequency distribution of leading digits in many real-life sets of numerical data. The law states that in many naturally occurring collections of numbers, the leading digit is likely to be small. In sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time. Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.

In statistics and in probability theory, distance correlation or distance covariance is a measure of dependence between two paired random vectors of arbitrary, not necessarily equal, dimension. The population distance correlation coefficient is zero if and only if the random vectors are independent. Thus, distance correlation measures both linear and nonlinear association between two random variables or random vectors. This is in contrast to Pearson's correlation, which can only detect linear association between two random variables.

In the statistical theory of estimation, the German tank problem consists of estimating the maximum of a discrete uniform distribution from sampling without replacement. In simple terms, suppose there exists an unknown number of items which are sequentially numbered from 1 to N. A random sample of these items is taken and their sequence numbers observed; the problem is to estimate N from these observed numbers.

Given random variables , that are defined on a probability space, the joint probability distribution for is a probability distribution that gives the probability that each of falls in any particular range or discrete set of values specified for that variable. In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to any number of random variables, giving a multivariate distribution.

In statistics, the monotone likelihood ratio property is a property of the ratio of two probability density functions (PDFs). Formally, distributions ƒ(x) and g(x) bear the property if

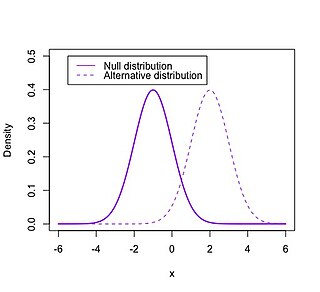
In statistical hypothesis testing, the null distribution is the probability distribution of the test statistic when the null hypothesis is true. For example, in an F-test, the null distribution is an F-distribution. Null distribution is a tool scientists often use when conducting experiments. The null distribution is the distribution of two sets of data under a null hypothesis. If the results of the two sets of data are not outside the parameters of the expected results, then the null hypothesis is said to be true.

In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four.

In probability theory and statistics, there are several relationships among probability distributions. These relations can be categorized in the following groups:One distribution is a special case of another with a broader parameter space Transforms ; Combinations ; Approximation (limit) relationships; Compound relationships ; Duality; Conjugate priors.

In statistics, the concept of the shape of a probability distribution arises in questions of finding an appropriate distribution to use to model the statistical properties of a population, given a sample from that population. The shape of a distribution may be considered either descriptively, using terms such as "J-shaped", or numerically, using quantitative measures such as skewness and kurtosis.

In statistics, a truncated distribution is a conditional distribution that results from restricting the domain of some other probability distribution. Truncated distributions arise in practical statistics in cases where the ability to record, or even to know about, occurrences is limited to values which lie above or below a given threshold or within a specified range. For example, if the dates of birth of children in a school are examined, these would typically be subject to truncation relative to those of all children in the area given that the school accepts only children in a given age range on a specific date. There would be no information about how many children in the locality had dates of birth before or after the school's cutoff dates if only a direct approach to the school were used to obtain information.