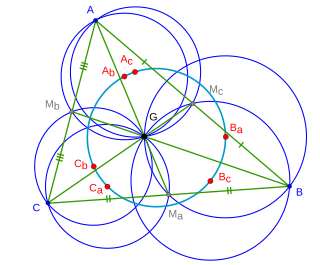
 W
WIn geometry, the Brocard circle for a triangle is a circle defined from a given triangle. It passes through the circumcenter and symmedian of the triangle, and is centered at the midpoint of the line segment joining them.
 W
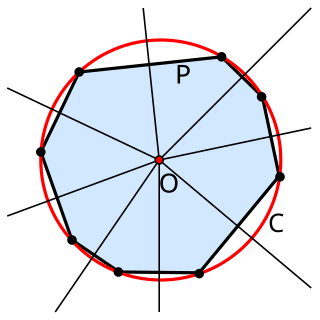
WIn geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
 W
WIn geometry, the Fuhrmann circle of a triangle, named after the German Wilhelm Fuhrmann (1833–1904), is the circle with a diameter of the line segment between the orthocenter and the Nagel point . This circle is identical with the circumcircle of the Fuhrmann triangle.
 W
WIn geometry, the GEOS circle is derived from the intersection of four lines that are associated with a generalized triangle: the Euler line, the Soddy line, the orthic axis and the Gergonne line. Note that the Euler line is orthogonal to the orthic axis and that the Soddy line is orthogonal to the Gergonne line.
 W
WIn geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
 W
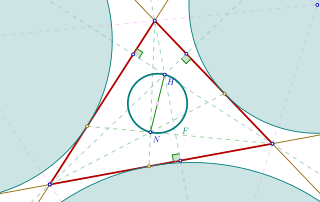
WIn geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle.
 W
WIn geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:The midpoint of each side of the triangle The foot of each altitude The midpoint of the line segment from each vertex of the triangle to the orthocenter.
 W
WIn geometry, the orthocentroidal circle of a non-equilateral triangle is the circle that has the triangle's orthocenter and its centroid at opposite ends of a diameter. This diameter also contains the triangle's nine-point center and is a subset of the Euler line, which also contains the circumcenter outside the orthocentroidal circle.
 W
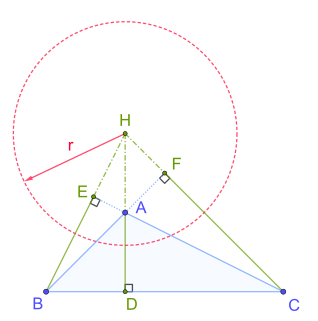
WIn geometry, the polar circle of a triangle is the circle whose center is the triangle's orthocenter and whose squared radius is
 W
WIn geometry, the incircle of the medial triangle of a triangle is the Spieker circle, named after 19th-century German geometer Theodor Spieker. Its center, the Spieker center, in addition to being the incenter of the medial triangle, is the center of mass of the uniform-density boundary of triangle. The Spieker center is also the point where all three cleavers of the triangle intersect each other.
 W
WIn Euclidean plane geometry, the van Lamoen circle is a special circle associated with any given triangle . It contains the circumcenters of the six triangles that are defined inside by its three medians.