 W
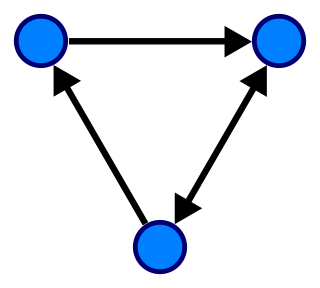
WIn mathematics, particularly graph theory, and computer science, a directed acyclic graph is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to sociology to computation (scheduling).
 W
WIn mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by edges, where the edges have a direction associated with them.
 W
WIn graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.
 W
WA feedback arc set (FAS) or feedback edge set is a set of edges which, when removed from the graph, leaves an acyclic graph. Put another way, it is a set containing at least one edge of every cycle in the graph. In graph theory, a directed graph may contain directed cycles, a closed one-way path of edges. In some applications, such cycles are undesirable, and we wish to eliminate them and obtain a directed acyclic graph (DAG). One way to do this is simply to drop edges from the graph to break the cycles.
 W
WIn mathematical logic, an implication graph is a skew-symmetric directed graph G = composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal u is true then the literal v is also true". Implication graphs were originally used for analyzing complex Boolean expressions.
 W
WThe Kautz graph is a directed graph of degree and dimension , which has vertices labeled by all possible strings of length which are composed of characters chosen from an alphabet containing distinct symbols, subject to the condition that adjacent characters in the string cannot be equal.
 W
WIn combinatorics and order-theoretic mathematics, a multitree may describe either of two equivalent structures: a directed acyclic graph (DAG) in which the set of vertices reachable from any vertex induces a tree, or a partially ordered set (poset) that does not have four items a, b, c, and d forming a diamond suborder with a ≤ b ≤ d and a ≤ c ≤ d but with b and c incomparable to each other.
 W
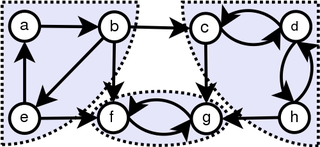
WIn the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time.
 W
WA tournament is a directed graph (digraph) obtained by assigning a direction for each edge in an undirected complete graph. That is, it is an orientation of a complete graph, or equivalently a directed graph in which every pair of distinct vertices is connected by a directed edge with any one of the two possible orientations.
 W
WIn the mathematical and algorithmic study of graph theory, the converse, transpose or reverse of a directed graph G is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in G. That is, if G contains an edge (u,v) then the converse/transpose/reverse of G contains an edge (v,u) and vice versa.
 W
WA wait-for graph in computer science is a directed graph used for deadlock detection in operating systems and relational database systems.