 W
WA fractal curve is, loosely, a mathematical curve whose shape retains the same general pattern of irregularity, regardless of how high it is magnified, that is, its graph takes the form of a fractal. In general, fractal curves are nowhere rectifiable curves — that is, they do not have finite length — and every subarc longer than a single point has infinite length.
 W
WA dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems. The dragon curve is probably most commonly thought of as the shape that is generated from repeatedly folding a strip of paper in half, although there are other curves that are called dragon curves that are generated differently.
 W
WThe Gosper curve, also known as Peano-Gosper Curve, named after Bill Gosper, also known as the flowsnake, is a space-filling curve whose limit set is rep-7. It is a fractal curve similar in its construction to the dragon curve and the Hilbert curve.
 W
WThe Hilbert curve is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling Peano curves discovered by Giuseppe Peano in 1890.
 W
WA Moore curve is a continuous fractal space-filling curve which is a variant of the Hilbert curve. Precisely, it is the loop version of the Hilbert curve, and it may be thought as the union of four copies of the Hilbert curves combined in such a way to make the endpoints coincide.
 W
WIn mathematics, an Osgood curve is a non-self-intersecting curve of positive area. More formally, these are curves in the Euclidean plane with positive two-dimensional Lebesgue measure.
In geometry, the Peano curve is the first example of a space-filling curve to be discovered, by Giuseppe Peano in 1890. Peano's curve is a surjective, continuous function from the unit interval onto the unit square, however it is not injective. Peano was motivated by an earlier result of Georg Cantor that these two sets have the same cardinality. Because of this example, some authors use the phrase "Peano curve" to refer more generally to any space-filling curve.
 W
WSierpiński curves are a recursively defined sequence of continuous closed plane fractal curves discovered by Wacław Sierpiński, which in the limit completely fill the unit square: thus their limit curve, also called the Sierpiński curve, is an example of a space-filling curve.
 W
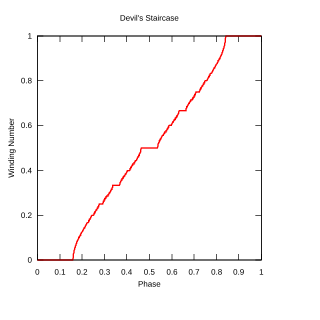
WIn mathematics, a real-valued function f on the interval [a, b] is said to be singular if it has the following properties:f is continuous on [a, b]. (**) there exists a set N of measure 0 such that for all x outside of N the derivative f ′(x) exists and is zero, that is, the derivative of f vanishes almost everywhere. f is non-constant on [a, b].
 W
WIn mathematics, the Weierstrass function is an example of a real-valued function that is continuous everywhere but differentiable nowhere. It is an example of a fractal curve. It is named after its discoverer Karl Weierstrass.
 W
WIn mathematical analysis and computer science, functions which are Z-order, Lebesgue curve, Morton space filling curve, Morton order or Morton code map multidimensional data to one dimension while preserving locality of the data points. It is named after Guy Macdonald Morton, who first applied the order to file sequencing in 1966. The z-value of a point in multidimensions is simply calculated by interleaving the binary representations of its coordinate values. Once the data are sorted into this ordering, any one-dimensional data structure can be used such as binary search trees, B-trees, skip lists or hash tables. The resulting ordering can equivalently be described as the order one would get from a depth-first traversal of a quadtree.