 W
WIn chemistry and quantum physics, quantum numbers describe values of conserved quantities in the dynamics of a quantum system. Quantum numbers correspond to eigenvalues of operators that commute with the Hamiltonian—quantities that can be known with precision at the same time as the system's energy—and their corresponding eigenspaces. Together, a specification of all of the quantum numbers of a quantum system fully characterize a basis state of the system, and can in principle be measured together.
 W
WThe Bohr–Einstein debates were a series of public disputes about quantum mechanics between Albert Einstein and Niels Bohr. Their debates are remembered because of their importance to the philosophy of science. An account of the debates was written by Bohr in an article titled "Discussions with Einstein on Epistemological Problems in Atomic Physics". Despite their differences of opinion regarding quantum mechanics, Bohr and Einstein had a mutual admiration that was to last the rest of their lives.
 W
WA time crystal or space-time crystal is a state of matter that repeats in time, as well as in space. Normal three-dimensional crystals have a repeating pattern in space, but remain unchanged as time passes. Time crystals repeat themselves in time as well, leading the crystal to change from moment to moment.
 W
WQuantum decoherence is the loss of quantum coherence. In quantum mechanics, particles such as electrons are described by a wave function, a mathematical representation of the quantum state of a system; a probabilistic interpretation of the wave function is used to explain various quantum effects. As long as there exists a definite phase relation between different states, the system is said to be coherent. A definite phase relationship is necessary to perform quantum computing on quantum information encoded in quantum states. Coherence is preserved under the laws of quantum physics.
 W
WThe Einstein–Podolsky–Rosen paradox is a thought experiment proposed by physicists Albert Einstein, Boris Podolsky and Nathan Rosen (EPR), with which they argued that the description of physical reality provided by quantum mechanics was incomplete. In a 1935 paper titled "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?", they argued for the existence of "elements of reality" that were not part of quantum theory, and speculated that it should be possible to construct a theory containing them. Resolutions of the paradox have important implications for the interpretation of quantum mechanics.
 W
WThe many-worlds interpretation (MWI) is an interpretation of quantum mechanics that asserts that the universal wavefunction is objectively real, and that there is no wavefunction collapse. This implies that all possible outcomes of quantum measurements are physically realized in some "world" or universe. In contrast to some other interpretations, such as the Copenhagen interpretation, the evolution of reality as a whole in MWI is rigidly deterministic. Many-worlds is also called the relative state formulation or the Everett interpretation, after physicist Hugh Everett, who first proposed it in 1957. Bryce DeWitt popularized the formulation and named it many-worlds in the 1960s and 1970s.
 W
WIn theoretical physics, the pilot wave theory, also known as Bohmian mechanics, was the first known example of a hidden-variable theory, presented by Louis de Broglie in 1927. Its more modern version, the de Broglie–Bohm theory, interprets quantum mechanics as a deterministic theory, avoiding troublesome notions such as wave–particle duality, instantaneous wave function collapse, and the paradox of Schrödinger's cat. To solve these problems, the theory is inherently nonlocal.
 W
WIn quantum mechanics, a probability amplitude is a complex number used in describing the behaviour of systems. The modulus squared of this quantity represents a probability density.
 W
WIn quantum mechanics, Schrödinger's cat is a thought experiment that illustrates an apparent paradox of quantum superposition. In the thought experiment, a hypothetical cat may be considered simultaneously both alive and dead as a result of being linked to a random subatomic event that may or may not occur.
 W
WA symmetric, informationally complete, positive operator-valued measure (SIC-POVM) is a special case of a generalized measurement on a Hilbert space, used in the field of quantum mechanics. A measurement of the prescribed form satisfies certain defining qualities that makes it an interesting candidate for a "standard quantum measurement", utilized in the study of foundational quantum mechanics, most notably in QBism. Furthermore, it has been shown that applications exist in quantum state tomography and quantum cryptography, and a possible connection has been discovered with Hilbert's twelfth problem.
 W
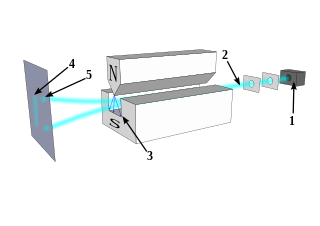
WThe Stern–Gerlach experiment demonstrated that the spatial orientation of angular momentum is quantized. Thus an atomic-scale system was shown to have intrinsically quantum properties. In the original experiment, silver atoms were sent through a spatially varying magnetic field, which deflected them before they struck a detector screen, such as a glass slide. Particles with non-zero magnetic moment are deflected, due to the magnetic field gradient, from a straight path. The screen reveals discrete points of accumulation, rather than a continuous distribution, owing to their quantized spin. Historically, this experiment was decisive in convincing physicists of the reality of angular-momentum quantization in all atomic-scale systems.