 W
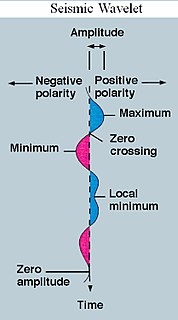
WA wavelet is a wave-like oscillation with an amplitude that begins at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one recorded by a seismograph or heart monitor. Generally, wavelets are intentionally crafted to have specific properties that make them useful for signal processing.
 W
WCoiflets are discrete wavelets designed by Ingrid Daubechies, at the request of Ronald Coifman, to have scaling functions with vanishing moments. The wavelet is near symmetric, their wavelet functions have vanishing moments and scaling functions , and has been used in many applications using Calderón–Zygmund operators.
 W
WIn numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.
 W
WIn signal processing, a filter bank is an array of band-pass filters that separates the input signal into multiple components, each one carrying a single frequency sub-band of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components differently and recombine them into a modified version of the original signal. The process of decomposition performed by the filter bank is called analysis ; the output of analysis is referred to as a subband signal with as many subbands as there are filters in the filter bank. The reconstruction process is called synthesis, meaning reconstitution of a complete signal resulting from the filtering process.
 W
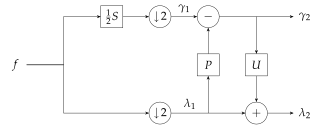
WThe generalized lifting scheme was developed by Joel Solé and Philippe Salembier and published in Solé's PhD dissertation. It is based on the classical lifting scheme and generalizes it by breaking out a restriction hidden in the scheme structure. The classical lifting scheme has three kinds of operations:A lazy wavelet transform splits signal in two new signals: the odd-samples signal denoted by and the even-samples signal denoted by . A prediction step computes a prediction for the odd samples, based on the even samples. This prediction is subtracted from the odd samples, creating an error signal . An update step recalibrates the low-frequency branch with some of the energy removed during subsampling. In the case of classical lifting, this is used in order to "prepare" the signal for the next prediction step. It uses the predicted odd samples to prepare the even ones . This update is subtracted from the even samples, producing the signal denoted by .
 W
WJPEG 2000 (JP2) is an image compression standard and coding system. It was developed from 1997 to 2000 by a Joint Photographic Experts Group committee chaired by Touradj Ebrahimi, with the intention of superseding their original discrete cosine transform (DCT) based JPEG standard with a newly designed, wavelet-based method. The standardized filename extension is .jp2 for ISO/IEC 15444-1 conforming files and .jpx for the extended part-2 specifications, published as ISO/IEC 15444-2. The registered MIME types are defined in RFC 3745. For ISO/IEC 15444-1 it is image/jp2.
 W
WThe lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform (DWT). In an implementation, it is often worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform. This is then called the second-generation wavelet transform. The technique was introduced by Wim Sweldens.
 W
WThe Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. As a type of a continuous wavelet, it has been applied in a number of cases, such as in adaptive filters, fractal random fields, and multi-fault classification.
PGF is a wavelet-based bitmapped image format that employs lossless and lossy data compression. PGF was created to improve upon and replace the JPEG format. It was developed at the same time as JPEG 2000 but with a focus on speed over compression ratio.
 W
WIn the mathematical theory of wavelets, a spline wavelet is a wavelet constructed using a spline function. There are different types of spline wavelets. The interpolatory spline wavelets introduced by C.K. Chui and J.Z. Wang are based on a certain spline interpolation formula. Though these wavelets are orthogonal, they do not have compact supports. There is a certain class of wavelets, unique in some sense, constructed using B-splines and having compact supports. Even though these wavelets are not orthogonal they have some special properties that have made them quite popular. The terminology spline wavelet is sometimes used to refer to the wavelets in this class of spline wavelets. These special wavelets are also called B-spline wavelets and cardinal B-spline wavelets. The Battle-Lemarie wavelets are also wavelets constructed using spline functions.
 W
WIn mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.