12 Unsolved problems in graph theory

In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of his many conjectures in graph coloring theory. The conjecture states that, among all graphs requiring colors, the complete graph is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than , then, according to the conjecture, it may be colored with fewer than colors.

In graph theory, Conway's 99-graph problem is an unsolved problem asking whether there exists an undirected graph with 99 vertices, in which each two adjacent vertices have exactly one common neighbor, and in which each two non-adjacent vertices have exactly two common neighbors. Equivalently, every edge should be part of a unique triangle and every non-adjacent pair should be one of the two diagonals of a unique 4-cycle. John Horton Conway offered a $1000 prize for its solution.

In graph-theoretic mathematics, a cycle double cover is a collection of cycles in an undirected graph that together include each edge of the graph exactly twice. For instance, for any polyhedral graph, the faces of a convex polyhedron that represents the graph provide a double cover of the graph: each edge belongs to exactly two faces.

In graph theory, the Erdős–Faber–Lovász conjecture is an unsolved problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:If k complete graphs, each having exactly k vertices, have the property that every pair of complete graphs has at most one shared vertex, then the union of the graphs can be colored with k colors.

In graph theory, the unproven Erdős–Gyárfás conjecture, made in 1995 by the prolific mathematician Paul Erdős and his collaborator András Gyárfás, states that every graph with minimum degree 3 contains a simple cycle whose length is a power of two. Erdős offered a prize of $100 for proving the conjecture, or $50 for a counterexample; it is one of many conjectures of Erdős.

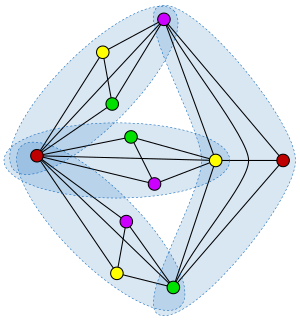
In graph theory, the Hadwiger conjecture states that if G is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

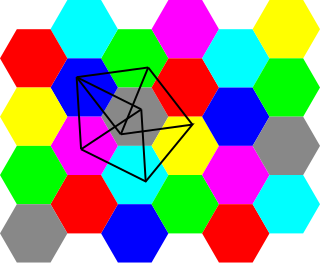
In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance 1 from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 5, 6 or 7. The correct value may depend on the choice of axioms for set theory.

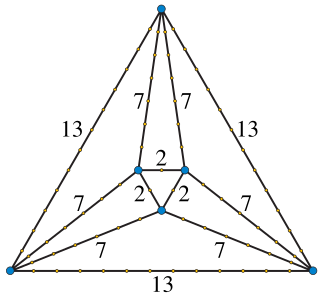
In mathematics, Harborth's conjecture states that every planar graph has a planar drawing in which every edge is a straight segment of integer length. This conjecture is named after Heiko Harborth, and would strengthen Fáry's theorem on the existence of straight-line drawings for every planar graph. For this reason, a drawing with integer edge lengths is also known as an integral Fáry embedding. Despite much subsequent research, Harborth's conjecture remains unsolved.

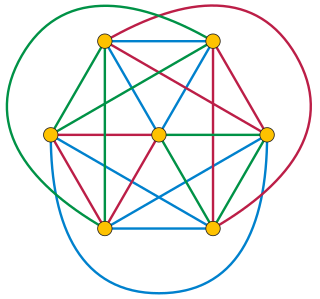
The Oberwolfach problem is an unsolved problem in mathematics that may be formulated either as a problem of scheduling seating assignments for diners, or more abstractly as a problem in graph theory, on the edge cycle covers of complete graphs. It is named after the Mathematical Research Institute of Oberwolfach, where the problem was posed in 1967 by Gerhard Ringel.

Sumner's conjecture states that every orientation of every -vertex tree is a subgraph of every -vertex tournament. David Sumner, a graph theorist at the University of South Carolina, conjectured in 1971 that tournaments are universal graphs for polytrees. The conjecture was proven for all large by Daniela Kühn, Richard Mycroft, and Deryk Osthus.

In mathematics, Szymanski's conjecture, named after Ted H. Szymanski (1989), states that every permutation on the n-dimensional doubly directed hypercube graph can be routed with edge-disjoint paths. That is, if the permutation σ matches each vertex v to another vertex σ(v), then for each v there exists a path in the hypercube graph from v to σ(v) such that no two paths for two different vertices u and v use the same edge in the same direction.

In the mathematics of graph drawing, Turán's brick factory problem asks for the minimum number of crossings in a drawing of a complete bipartite graph. The problem is named after Pál Turán, who formulated it while being forced to work in a brick factory during World War II.