13 Divisor function

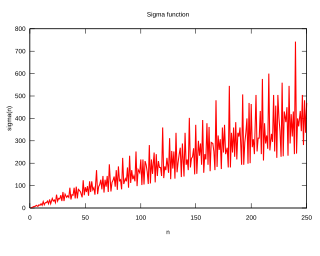
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

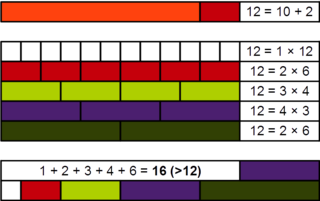
In number theory, an abundant number or excessive number is a number that is smaller than the sum of its proper divisors. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example.

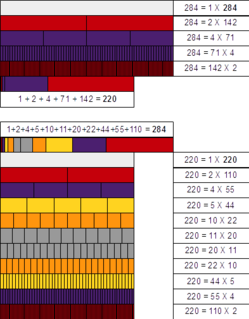
In mathematics, an almost perfect number (sometimes also called slightly defective or least deficient number) is a natural number n such that the sum of all divisors of n (the sum-of-divisors function σ(n)) is equal to 2n − 1, the sum of all proper divisors of n, s(n) = σ(n) − n, then being equal to n − 1. The only known almost perfect numbers are powers of 2 with non-negative exponents (sequence A000079 in the OEIS). Therefore the only known odd almost perfect number is 20 = 1, and the only known even almost perfect numbers are those of the form 2k for some positive number k; however, it has not been shown that all almost perfect numbers are of this form. It is known that an odd almost perfect number greater than 1 would have at least six prime factors.

Amicable numbers are two different numbers related in such a way that the sum of the proper divisors of each is equal to the other number.

In number theory, an arithmetic number is an integer for which the average of its positive divisors is also an integer. For instance, 6 is an arithmetic number because the average of its divisors is

In mathematics, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Formally, a number n is colossally abundant if and only if there is an ε > 0 such that for all k > 1,

In number theory, a deficient number or defective number is a number n for which the sum of divisors of ‘’n’’ is less than 2n. Equivalently, it is a number for which the sum of proper divisors is less than n. For example, the proper divisors of 8 are 1, 2, and 4, and their sum is less than 8, so 8 is deficient.

In mathematics, a highly abundant number is a natural number with the property that the sum of its divisors is greater than the sum of the divisors of any smaller natural number.

In mathematics, a multiply perfect number is a generalization of a perfect number.

In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number.

In mathematics a primitive abundant number is an abundant number whose proper divisors are all deficient numbers.

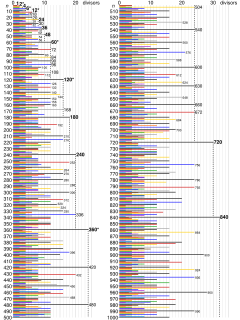
The tables below list all of the divisors of the numbers 1 to 1000.

In number theory, a weird number is a natural number that is abundant but not semiperfect.