W

An acnode is an isolated point in the solution set of a polynomial equation in two real variables. Equivalent terms are "isolated point or hermit point".

W

An atriphtaloid, also called an atriphtothlassic curve, is type of sextic plane curve. It is given by the equation

W

In mathematics, a bullet-nose curve is a unicursal quartic curve with three inflection points, given by the equation

W

In mathematics, the algebraic butterfly curve is a plane algebraic curve of degree six, given by the equation]

W

In algebraic geometry, the Cayley surface, named after Arthur Cayley, is a cubic nodal surface in 3-dimensional projective space with four conical points. It can be given by the equation

W

In geometry, the Fermat cubic, named after Pierre de Fermat, is a surface defined by

W

In mathematics, the Labs septic surface is a degree-7 (septic) nodal surface with 99 nodes found by Labs (2006). As of 2015, it has the largest known number of nodes of a degree-7 surface, though this number is still less than the best known upper bound of 104 nodes given by Giventalʹ (1983) and Varchenko (1983).

W

Lamé's special quartic, named after Gabriel Lamé, is the graph of the equation

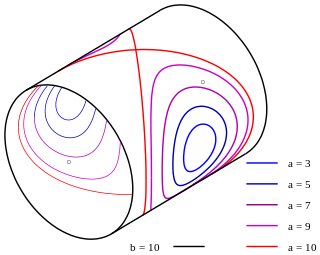
W

In geometry, Plücker's conoid is a ruled surface named after the German mathematician Julius Plücker. It is also called a conical wedge or cylindroid; however, the latter name is ambiguous, as "cylindroid" may also refer to an elliptic cylinder.

W

A Steinmetz curve is the curve of intersection of two right circular cylinders of radii and whose axes intersect perpendicularly. In case of the Steimetz curves are the edges of a Steinmetz solid. If the cylinder axes are the x- and y-axes and , then the Steinmetz curves are given by the parametric equations:

W

In algebraic geometry, a tetrahedroid is a special kind of Kummer surface studied by Cayley (1846), with the property that the intersections with the faces of a fixed tetrahedron are given by two conics intersecting in four nodes. Tetrahedroids generalize Fresnel's wave surface.

W

In algebraic geometry, a Togliatti surface is a nodal surface of degree five with 31 nodes. The first examples were constructed by Eugenio G. Togliatti (1940). Arnaud Beauville (1980) proved that 31 is the maximum possible number of nodes for a surface of this degree, showing this example to be optimal.

W

In mathematics, a trident curve is any member of the family of curves that have the formula:

W

In geometry, the Tschirnhausen cubic, or Tschirnhaus' cubic is a plane curve defined, in its left-opening form, by the polar equation

W

In algebraic geometry and string theory, the phenomenon of wall-crossing describes the discontinuous change of a certain quantity, such as an integer geometric invariant, an index or a space of BPS state, across a codimension-one wall in a space of stability conditions, a so-called wall of marginal stability.