15 Pentagonal tilings

In geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.

In geometry, the binary tiling is a tiling of the hyperbolic plane, resembling a quadtree over the Poincaré half-plane model of the hyperbolic plane. It was first studied in 1974 by Károly Böröczky.

In geometry, a Cairo pentagonal tiling is a tessellation of the Euclidean plane by congruent convex pentagons, formed by overlaying two tessellations of the plane by hexagons and named for its use as a paving design in Cairo. It is also called MacMahon's net after Percy Alexander MacMahon, who depicted it in his 1921 publication New Mathematical Pastimes. John Horton Conway calls it a 4-fold pentille.

In 2-dimensional hyperbolic geometry, the infinite-order pentagonal tiling is a regular tiling. It has Schläfli symbol of {5,∞}. All vertices are ideal, located at "infinity", seen on the boundary of the Poincaré hyperbolic disk projection.

A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(p,q). Dihedra have also been called bihedra, flat polyhedra, or doubly covered polygons.

A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals. It is represented by the Schläfli symbol {5,3}.

In geometry, the order-4 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {5,4}. It can also be called a pentapentagonal tiling in a bicolored quasiregular form.

In geometry, the order-5 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {5,5}, constructed from five pentagons around every vertex. As such, it is self-dual.

The order-5 truncated pentagonal hexecontahedron is a convex polyhedron with 72 faces: 60 hexagons and 12 pentagons triangular, with 210 edges, and 140 vertices. Its dual is the pentakis snub dodecahedron.

In geometry, the order-6 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {5,6}.

In geometry, the order-8 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {5,8}.

In geometry, the sphinx tiling is a tessellation of the plane using the "sphinx", a pentagonal hexiamond formed by gluing six equilateral triangles together. The resultant shape is named for its reminiscence to the Great Sphinx at Giza. A sphinx can be dissected into any square number of copies of itself, some of them mirror images, and repeating this process leads to a non-periodic tiling of the plane. The sphinx is therefore a rep-tile. It is one of few known pentagonal rep-tiles and is the only known pentagonal rep-tile whose sub-copies are equal in size.

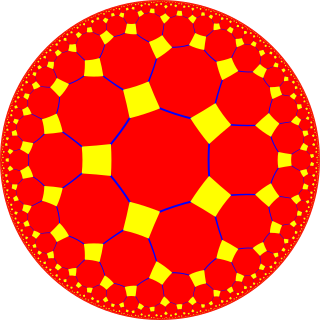
In geometry, the truncated order-4 pentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{5,4}.

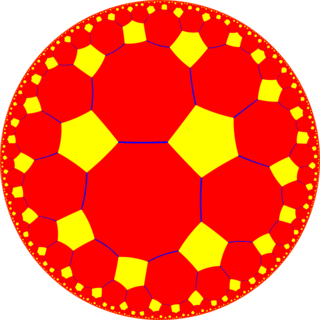
In geometry, the truncated order-5 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{5,5}, constructed from one pentagons and two decagons around every vertex.

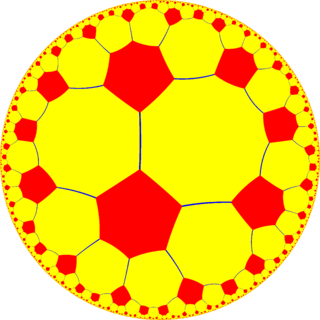
In geometry, the truncated order-6 pentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t1,2{6,5}.