15 Theorems in graph theory

In polyhedral combinatorics, a branch of mathematics, Balinski's theorem is a statement about the graph-theoretic structure of three-dimensional polyhedra and higher-dimensional polytopes. It states that, if one forms an undirected graph from the vertices and edges of a convex d-dimensional polyhedron or polytope, then the resulting graph is at least d-vertex-connected: the removal of any d − 1 vertices leaves a connected subgraph. For instance, for a three-dimensional polyhedron, even if two of its vertices are removed, for any pair of vertices there will still exist a path of vertices and edges connecting the pair.

In graph theory, Brooks' theorem states a relationship between the maximum degree of a graph and its chromatic number. According to the theorem, in a connected graph in which every vertex has at most Δ neighbors, the vertices can be colored with only Δ colors, except for two cases, complete graphs and cycle graphs of odd length, which require Δ + 1 colors.

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:

In graph theory, a branch of mathematics, Fleischner's theorem gives a sufficient condition for a graph to contain a Hamiltonian cycle. It states that, if G is a 2-vertex-connected graph, then the square of G is Hamiltonian. it is named after Herbert Fleischner, who published its proof in 1974.

In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. Since then the proof has gained wide acceptance, although some doubters remain.

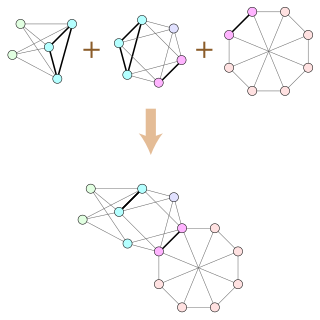
Frucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph. More strongly, for any finite group G there exist infinitely many non-isomorphic simple connected graphs such that the automorphism group of each of them is isomorphic to G.

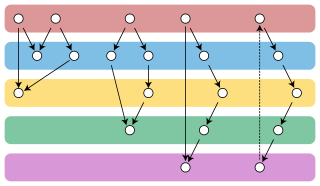
In graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations of its edges. It states that the minimum number of colors needed to properly color any graph G equals one plus the length of a longest path in an orientation of G chosen to minimize this path's length. The orientations for which the longest path has minimum length always include at least one acyclic orientation.

In graph theory, Grinberg's theorem is a necessary condition for a planar graph to contain a Hamiltonian cycle, based on the lengths of its face cycles. The result has been widely used to construct non-Hamiltonian planar graphs with further properties, such as to give new counterexamples to Tait's conjecture. This theorem was proved by Latvian mathematician Emanuel Grinberg in 1968.

In the mathematical field of graph theory, Grötzsch's theorem is the statement that every triangle-free planar graph can be colored with only three colors. According to the four-color theorem, every graph that can be drawn in the plane without edge crossings can have its vertices colored using at most four different colors, so that the two endpoints of every edge have different colors, but according to Grötzsch's theorem only three colors are needed for planar graphs that do not contain three mutually-adjacent vertices.

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.

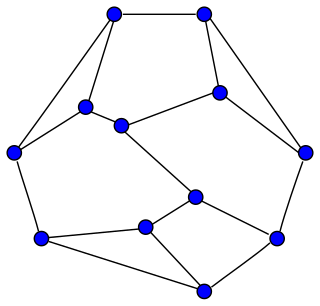
In graph theory and polyhedral combinatorics, areas of mathematics, Kotzig's theorem is the statement that every polyhedral graph has an edge whose two endpoints have total degree at most 13. An extreme case is the triakis icosahedron, where no edge has smaller total degree. The result is named after Anton Kotzig, who published it in 1955 in the dual form that every convex polyhedron has two adjacent faces with a total of at most 13 sides. It was named and popularized in the west in the 1970s by Branko Grünbaum.

In graph theory, Kuratowski's theorem is a mathematical forbidden graph characterization of planar graphs, named after Kazimierz Kuratowski. It states that a finite graph is planar if and only if it does not contain a subgraph that is a subdivision of K5 or of K3,3.

Ore's theorem is a result in graph theory proved in 1960 by Norwegian mathematician Øystein Ore. It gives a sufficient condition for a graph to be Hamiltonian, essentially stating that a graph with sufficiently many edges must contain a Hamilton cycle. Specifically, the theorem considers the sum of the degrees of pairs of non-adjacent vertices: if every such pair has a sum that at least equals the total number of vertices in the graph, then the graph is Hamiltonian.

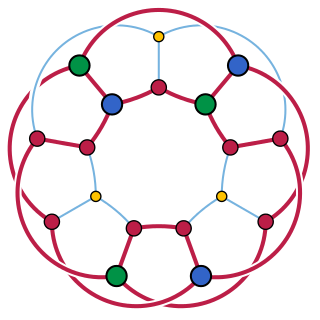
In the mathematical discipline of graph theory, Petersen's theorem, named after Julius Petersen, is one of the earliest results in graph theory and can be stated as follows:Petersen's Theorem. Every cubic, bridgeless graph contains a perfect matching.

In graph theory, Wagner's theorem is a mathematical forbidden graph characterization of planar graphs, named after Klaus Wagner, stating that a finite graph is planar if and only if its minors include neither K5 nor K3,3. This was one of the earliest results in the theory of graph minors and can be seen as a forerunner of the Robertson–Seymour theorem.