W

In mathematics, affine geometry is what remains of Euclidean geometry when not using the metric notions of distance and angle.

W

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.

W

In Euclidean geometry, an affine transformation, or an affinity, is a geometric transformation that preserves lines and parallelism.

W

The Barnsley fern is a fractal named after the British mathematician Michael Barnsley who first described it in his book Fractals Everywhere. He made it to resemble the black spleenwort, Asplenium adiantum-nigrum.

W

In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex. The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.

W

In mathematics and physics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin.

W

Ceva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O, to meet opposite sides at D, E and F respectively. Then, using signed lengths of segments,

W

In geometry, an equidissection is a partition of a polygon into triangles of equal area. The study of equidissections began in the late 1960s with Monsky's theorem, which states that a square cannot be equidissected into an odd number of triangles. In fact, most polygons cannot be equidissected at all.

W

In geometry, a hyperplane is a subspace whose dimension is one less than that of its ambient space. If a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. This notion can be used in any general space in which the concept of the dimension of a subspace is defined.

W

Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC, and AB at points D, E, and F respectively, with D, E, and F distinct from A, B, and C, then

W

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

W

In geometry, the Minkowski sum of two sets of position vectors A and B in Euclidean space is formed by adding each vector in A to each vector in B, i.e., the set

W

In plane geometry, a triangle ABC contains a triangle having one-seventh of the area of ABC, which is formed as follows: the sides of this triangle lie on cevians p, q, r wherep connects A to a point on BC that is one-third the distance from B to C, q connects B to a point on CA that is one-third the distance from C to A, r connects C to a point on AB that is one-third the distance from A to B.

W

In geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the pairwise intersections of three cevians. The theorem states that if in triangle points , , and lie on segments , , and , then writing , , and , the signed area of the triangle formed by the cevians , , and is the area of triangle times

W

In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a rotation or shear mapping.

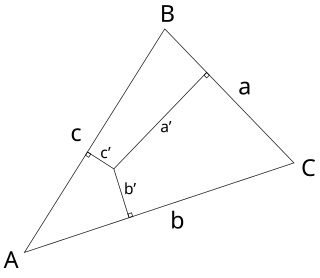
W

In geometry, the trilinear coordinates x:y:z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x:y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y:z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z:x and vertices C and A.