16 Circle packing

In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:

In mathematics, an Apollonian gasket or Apollonian net is a fractal generated starting from a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek mathematician Apollonius of Perga.

Circle packing in a circle is a two-dimensional packing problem with the objective of packing unit circles into the smallest possible larger circle.

Circle packing in an equilateral triangle is a packing problem in discrete mathematics where the objective is to pack n unit circles into the smallest possible equilateral triangle. Optimal solutions are known for n < 13 and for any triangular number of circles, and conjectures are available for n < 28.

Circle packing in a right isosceles triangle is a packing problem where the objective is to pack n unit circles into the smallest possible isosceles right triangle.

In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.

In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane, each tangent to six others. The sequences of circles linked to each other through opposite points of tangency lie on logarithmic spirals having, in general, three different shapes of spirals.

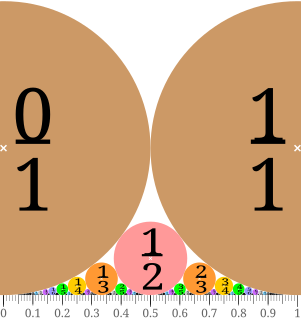
In mathematics, a Ford circle is a circle with center at and radius where is an irreducible fraction, i.e. and are coprime integers. Each Ford circle is tangent to the horizontal axis and any two Ford circles are either tangent or disjoint from each other.

In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle.

In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point. Not every polyhedron has a midsphere, but for every polyhedron there is a combinatorially equivalent polyhedron, the canonical polyhedron, that does have a midsphere.

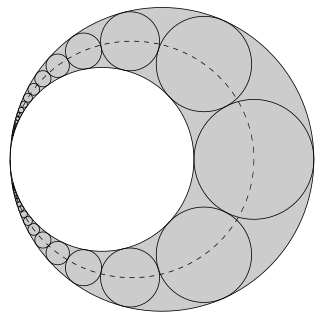
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.

In geometric graph theory, a penny graph is a contact graph of unit circles. That is, it is an undirected graph whose vertices can be represented by unit circles, with no two of these circles crossing each other, and with two adjacent vertices if and only if they are represented by tangent circles. More simply, they are the graphs formed by arranging pennies in a non-overlapping way on a flat surface, making a vertex for each penny, and making an edge for each two pennies that touch.

In the geometry of circle packings in the Euclidean plane, the ring lemma gives a lower bound on the sizes of adjacent circles in a circle packing.

In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles, where n is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual closed Steiner chains, the first and last (nth) circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles α and β do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola, respectively.

In geometry, the Tammes problem is a problem in packing a given number of circles on the surface of a sphere such that the minimum distance between circles is maximized. It is named after a Dutch botanist who posed the problem in 1930 while studying the distribution of pores on pollen grains. It can be viewed as a particular special case of the generalized Thomson problem.