16 Convex analysis

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory.

In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.

In mathematics, a real-valued function defined on an n-dimensional interval is called convex if the line segment between any two points on the graph of the function lies above the graph between the two points. Equivalently, a function is convex if its epigraph is a convex set. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include the quadratic function and the exponential function . In simple terms, a convex function refers to a function that is in the shape of a cup , and a concave function is in the shape of a cap .

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points, it contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersect every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

In geometry, a Danzer set is a set of points that touches every convex body of unit volume. Ludwig Danzer asked whether it is possible for such a set to have bounded density. Several variations of this problem remain unsolved.

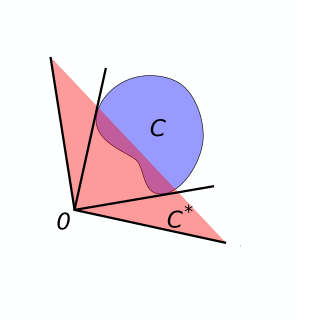
Dual cone and polar cone are closely related concepts in convex analysis, a branch of mathematics.

In mathematics, the epigraph or supergraph of a function f : Rn → R is the set of points lying on or above its graph:

In convex analysis, the Fenchel–Moreau theorem or Fenchel biconjugation theorem is a theorem which gives necessary and sufficient conditions for a function to be equal to its biconjugate. This is in contrast to the general property that for any function . This can be seen as a generalization of the bipolar theorem. It is used in duality theory to prove strong duality.

In complex analysis, a branch of mathematics, the Gauss–Lucas theorem gives a geometrical relation between the roots of a polynomial P and the roots of its derivative P′. The set of roots of a real or complex polynomial is a set of points in the complex plane. The theorem states that the roots of P′ all lie within the convex hull of the roots of P, that is the smallest convex polygon containing the roots of P. When P has a single root then this convex hull is a single point and when the roots lie on a line then the convex hull is a segment of this line. The Gauss–Lucas theorem, named after Carl Friedrich Gauss and Félix Lucas, is similar in spirit to Rolle's theorem.

In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations.

In mathematics and physics, the Legendre transformation, named after Adrien-Marie Legendre, is an involutive transformation on the real-valued convex functions of one real variable. In physical problems, it is used to convert functions of one quantity into functions of the conjugate quantity. In this way, it is commonly used in classical mechanics to derive the Hamiltonian formalism out of the Lagrangian formalism and in thermodynamics to derive the thermodynamic potentials, as well as in the solution of differential equations of several variables.

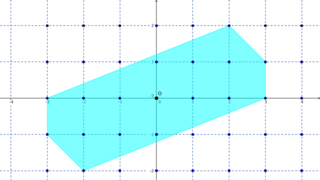
In Euclidean geometry, linear separability is a property of two sets of points. This is most easily visualized in two dimensions by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are linearly separable if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if the line is replaced by a hyperplane.

In mathematics, Minkowski's theorem is the statement that every convex set in which is symmetric with respect to the origin and which has volume greater than contains a non-zero integer point. The theorem was proved by Hermann Minkowski in 1889 and became the foundation of the branch of number theory called the geometry of numbers. It can be extended from the integers to any lattice and to any symmetric convex set with volume greater than , where denotes the covolume of the lattice.

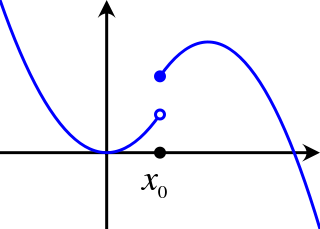
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set. For a function of a single variable, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.

Ralph Tyrrell Rockafellar is an American mathematician and one of the leading scholars in optimization theory and related fields of analysis and combinatorics. He is the author of four major books including the landmark text “Convex Analysis” (1970), which has been cited more than 27000 times according to Google Scholar and remains the standard reference on the subject, and "Variational Analysis" for which the authors received the Frederick W. Lanchester Prize from the Institute for Operations Research and the Management Sciences (INFORMS).