16 Curvature (mathematics)

In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.

The calculus of moving surfaces (CMS) is an extension of the classical tensor calculus to deforming manifolds. Central to the CMS is the Tensorial Time Derivative whose original definition was put forth by Jacques Hadamard. It plays the role analogous to that of the covariant derivative on differential manifolds. in that it produces a tensor when applied to a tensor.

In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension greater than 2 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define curvature for these manifolds, now known as the Riemann curvature tensor. Similar notions have found applications everywhere in differential geometry.

In mathematics, a knee of a curve is a point where the curve visibly bends, specifically from high slope to low slope, or in the other direction. This is particularly used in optimization, where a knee point is the optimum point for some decision, for example when there is an increasing function and a trade-off between the benefit and the cost : the knee is where the benefit is no longer increasing rapidly, and is no longer worth the cost of further increases – a cutoff point of diminishing returns.

In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a continuous, differentiable curve in three-dimensional Euclidean space ℝ3, or the geometric properties of the curve itself irrespective of any motion. More specifically, the formulas describe the derivatives of the so-called tangent, normal, and binormal unit vectors in terms of each other. The formulas are named after the two French mathematicians who independently discovered them: Jean Frédéric Frenet, in his thesis of 1847, and Joseph Alfred Serret in 1851. Vector notation and linear algebra currently used to write these formulas were not yet in use at the time of their discovery.

In differential geometry, the Gaussian curvature or Gauss curvature Κ of a surface at a point is the product of the principal curvatures, κ1 and κ2, at the given point:

In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections, the associated holonomy is a type of monodromy and is an inherently global notion. For curved connections, holonomy has nontrivial local and global features.

In mathematics, a knee of a curve is a point where the curve visibly bends, specifically from high slope to low slope, or in the other direction. This is particularly used in optimization, where a knee point is the optimum point for some decision, for example when there is an increasing function and a trade-off between the benefit and the cost : the knee is where the benefit is no longer increasing rapidly, and is no longer worth the cost of further increases – a cutoff point of diminishing returns.

In the mathematical field of differential geometry, the Levi-Civita parallelogramoid is a quadrilateral in a curved space whose construction generalizes that of a parallelogram in the Euclidean plane. It is named for its discoverer, Tullio Levi-Civita. Like a parallelogram, two opposite sides AA′ and BB′ of a parallelogramoid are parallel and the same length as each other, but the fourth side A′B′ will not in general be parallel to or the same length as the side AB, although it will be straight.

In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.

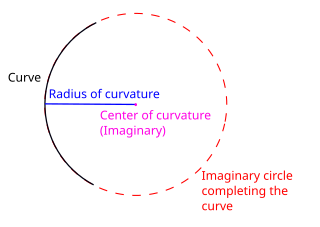
In differential geometry, the radius of curvature, R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.

In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold, that measures the extent to which the metric tensor is not locally isometric to that of Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.

Sinuosity, sinuosity index, or sinuosity coefficient of a continuously differentiable curve having at least one inflection point is the ratio of the curvilinear length and the Euclidean distance between the end points of the curve. This dimensionless quantity can also be rephrased as the "actual path length" divided by the "shortest path length" of a curve. The value ranges from 1 to infinity.

In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet–Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves. In the geometry of surfaces, the geodesic torsion describes how a surface twists about a curve on the surface. The companion notion of curvature measures how moving frames "roll" along a curve "without twisting".

In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arc length: