16 Lattice theory

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included. Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts; see Korte et al. (1991) for a comprehensive survey of antimatroid theory with many additional references.

In the mathematical discipline of order theory, a complemented lattice is a bounded lattice, in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0. Complements need not be unique.

In mathematics, the Dedekind numbers are a rapidly growing sequence of integers named after Richard Dedekind, who defined them in 1897. The Dedekind number M(n) counts the number of monotone boolean functions of n variables. Equivalently, it counts the number of antichains of subsets of an n-element set, the number of elements in a free distributive lattice with n generators, or the number of abstract simplicial complexes with n elements.

In the theory of lattices, the dual lattice is a construction analogous to that of a dual vector space. In certain respects, the geometry of the dual lattice of a lattice is the reciprocal of the geometry of , a perspective which underlies many of its uses.

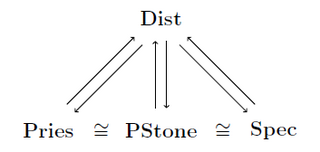
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This duality, which is originally also due to Marshall H. Stone, generalizes the well-known Stone duality between Stone spaces and Boolean algebras.

In mathematics, specifically order theory, the join of a subset S of a partially ordered set P is the supremum of S, denoted ⋁S, and similarly, the meet of S is the infimum, denoted ⋀S. In general, the join and meet of a subset of a partially ordered set need not exist. Join and meet are dual to one another with respect to order inversion.

In mathematics, the lattice of subgroups of a group is the lattice whose elements are the subgroups of , with the partial order relation being set inclusion. In this lattice, the join of two subgroups is the subgroup generated by their union, and the meet of two subgroups is their intersection.

The concept of a lattice arises in order theory, a branch of mathematics. The Hasse diagram below depicts the inclusion relationships among some important subclasses of lattices.

In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.

In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular lawa ≤ b implies a ∨ = ∧ b for every x,

In the branch of mathematics known as order theory, a semimodular lattice, is a lattice that satisfies the following condition:Semimodular lawa ∧ b <: a implies b <: a ∨ b.

A subsumption lattice is a mathematical structure used in the theoretical background of automated theorem proving and other symbolic computation applications.

In mathematics, a Tamari lattice, introduced by Dov Tamari (1962), is a partially ordered set in which the elements consist of different ways of grouping a sequence of objects into pairs using parentheses; for instance, for a sequence of four objects abcd, the five possible groupings are ( c)d, (ab)(cd), d, a( d), and a(b ). Each grouping describes a different order in which the objects may be combined by a binary operation; in the Tamari lattice, one grouping is ordered before another if the second grouping may be obtained from the first by only rightward applications of the associative law (xy)z = x(yz). For instance, applying this law with x = a, y = bc, and z = d gives the expansion d = a( d), so in the ordering of the Tamari lattice d ≤ a( d).

In musical tuning and harmony, the Tonnetz is a conceptual lattice diagram representing tonal space first described by Leonhard Euler in 1739. Various visual representations of the Tonnetz can be used to show traditional harmonic relationships in European classical music.

In mathematics, the Young–Fibonacci graph and Young–Fibonacci lattice, named after Alfred Young and Leonardo Fibonacci, are two closely related structures involving sequences of the digits 1 and 2. Any digit sequence of this type can be assigned a rank, the sum of its digits: for instance, the rank of 11212 is 1 + 1 + 2 + 1 + 2 = 7. As was already known in ancient India, the number of sequences with a given rank is a Fibonacci number. The Young–Fibonacci lattice is an infinite modular lattice having these digit sequences as its elements, compatible with this rank structure. The Young–Fibonacci graph is the graph of this lattice, and has a vertex for each digit sequence. As the graph of a modular lattice, it is a modular graph.

In mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who, in a series of papers On quantitative substitutional analysis, developed representation theory of the symmetric group. In Young's theory, the objects now called Young diagrams and the partial order on them played a key, even decisive, role. Young's lattice prominently figures in algebraic combinatorics, forming the simplest example of a differential poset in the sense of Stanley (1988). It is also closely connected with the crystal bases for affine Lie algebras.