16 Triangulation (geometry)

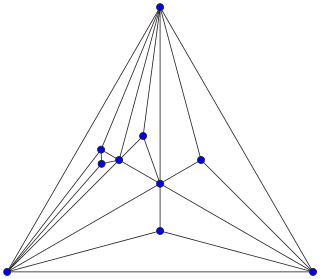
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

In mesh generation, Chew's second algorithm is a Delaunay refinement algorithm for creating quality constrained Delaunay triangulations. The algorithm takes a piecewise linear system (PLS) and returns a constrained Delaunay triangulation of only quality triangles where quality is defined by the minimum angle in a triangle. Developed by L. Paul Chew for meshing surfaces embedded in three-dimensional space, Chew's second algorithm has been adopted as a two-dimensional mesh generator due to practical advantages over Ruppert's algorithm in certain cases and is the default quality mesh generator implemented in the freely available Triangle package. Chew's second algorithm is guaranteed to terminate and produce a local feature size-graded meshes with minimum angle up to about 28.6 degrees.

In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.

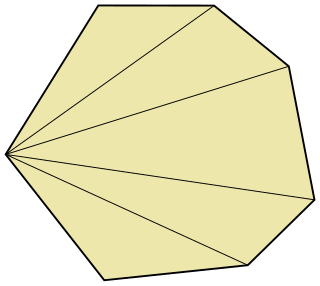
A fan triangulation is a simple way to triangulate a polygon by choosing a vertex and drawing diagonals to all of the other vertices of the polygon. Not every polygon can be triangulated this way, so this method is usually only used for convex polygons.

The Greedy Triangulation is a method to compute a polygon triangulation or a Point set triangulation using a greedy schema, which adds edges one by one to the solution in strict increasing order by length, with the condition that an edge cannot cut a previously inserted edge.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. The goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.

In computational geometry, a Pitteway triangulation is a point set triangulation in which the nearest neighbor of any point p within the triangulation is one of the vertices of the triangle containing p. Alternatively, it is a Delaunay triangulation in which each internal edge crosses its dual Voronoi diagram edge. Pitteway triangulations are named after Michael Pitteway, who studied them in 1973. Not every point set supports a Pitteway triangulation. When such a triangulation exists it is a special case of the Delaunay triangulation, and consists of the union of the Gabriel graph and convex hull.

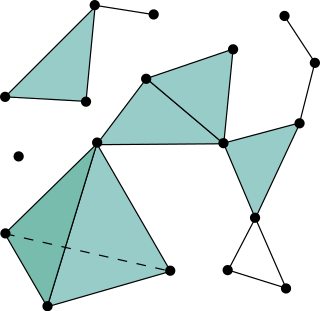
A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.

In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

A quasi-triangulation is a subdivision of a geometric object into simplices, where vertices are not points but arbitrary sloped line segments. This division is not a triangulation in the geometric sense. It is a topological triangulation, however. A quasi-triangulation may have some of the characteristics of a Delaunay triangulation.

In mesh generation, Ruppert's algorithm, also known as Delaunay refinement, is an algorithm for creating quality Delaunay triangulations. The algorithm takes a planar straight-line graph and returns a conforming Delaunay triangulation of only quality triangles. A triangle is considered poor-quality if it has a circumradius to shortest edge ratio larger than some prescribed threshold. Discovered by Jim Ruppert in the early 1990s, "Ruppert's algorithm for two-dimensional quality mesh generation is perhaps the first theoretically guaranteed meshing algorithm to be truly satisfactory in practice."

In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex.

A triangle mesh is a type of polygon mesh in computer graphics. It comprises a set of triangles that are connected by their common edges or corners.

A triangulated irregular network (TIN) is a representation of a continuous surface consisting entirely of triangular facets, used mainly as Discrete Global Grid in primary elevation modeling.

In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h: K → X.