17 Calculus

In mathematics, the binary logarithm is the power to which the number 2 must be raised to obtain the value n. That is, for any real number x,

The calculus of moving surfaces (CMS) is an extension of the classical tensor calculus to deforming manifolds. Central to the CMS is the Tensorial Time Derivative whose original definition was put forth by Jacques Hadamard. It plays the role analogous to that of the covariant derivative on differential manifolds. in that it produces a tensor when applied to a tensor.

Cours d'Analyse de l’École Royale Polytechnique; I.re Partie. Analyse algébrique is a seminal textbook in infinitesimal calculus published by Augustin-Louis Cauchy in 1821. The article follows the translation by Bradley and Sandifer in describing its contents.

In mathematics, a cubic function is a function of the form

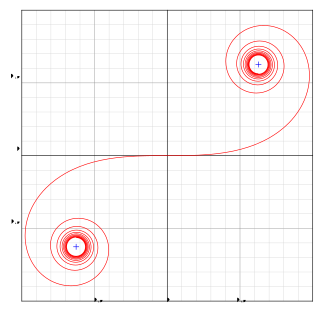
An Euler spiral is a curve whose curvature changes linearly with its curve length. Euler spirals are also commonly referred to as spiros, clothoids, or Cornu spirals.

In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series. They are named for the parity of the powers of the power functions which satisfy each condition: the function is an even function if n is an even integer, and it is an odd function if n is an odd integer.

In mathematics, infinitesimals or infinitesimal numbers are quantities that are closer to zero than any standard real number, but are not zero. They do not exist in the standard real number system, but do exist in many other number systems, such as the surreal numbers and hyperreal numbers, which can be thought of as the real numbers augmented with a system of infinitesimal quantities, as well as infinite quantities, which are the reciprocals of the infinitesimals.

In calculus and related areas of mathematics, a linear function from the real numbers to the real numbers is a function whose graph is a line in the plane. The characteristic property of linear functions is that when the input variable is changed, the change in the output is proportional to the change in the input.

In mathematical analysis, the maxima and minima of a function, known collectively as extrema, are the largest and smallest value of the function, either within a given range, or on the entire domain. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions.

"Nova Methodus pro Maximis et Minimis" is the first published work on the subject of calculus. It was published by Gottfried Leibniz in the Acta Eruditorum in October 1684. It is considered to be the birth of infinitesimal calculus.

A periodic function is a function that repeats its values at regular intervals, for example, the trigonometric functions, which repeat at intervals of 2π radians. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called aperiodic.

Regiomontanus' angle maximization problem

In mathematics, the Regiomontanus's angle maximization problem, is a famous optimization problem posed by the 15th-century German mathematician Johannes Müller. The problem is as follows:

Slope field is also called a direction field. The solutions of a first-order differential equation of a scalar function y(x) can be drawn in a 2-dimensional space with the x in horizontal and y in vertical direction. Possible solutions are functions y(x) drawn as solid curves. Sometimes it is too cumbersome solving the differential equation analytically. Then one can still draw the tangents of the function curves e.g. on a regular grid. The tangents are touching the functions at the grid points. However, the direction field is rather agnostic about chaotic aspects of the differential equation.

Thomae's function, named after Carl Johannes Thomae, has many names: the popcorn function, the raindrop function, the countable cloud function, the modified Dirichlet function, the ruler function, the Riemann function, or the Stars over Babylon. This real-valued function of a real variable can be defined as:

In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f(x) and f(y) be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, where the maximum distance between f(x) and f(y) may depend on x and y themselves.

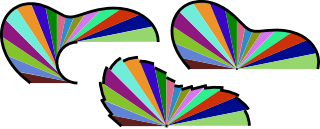
Visual calculus, invented by Mamikon Mnatsakanian, is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation, often reminiscent of what Martin Gardner calls "aha! solutions" or Roger Nelsen a proof without words.

John Wallis was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the royal court. He is credited with introducing the symbol ∞ to represent the concept of infinity. He similarly used 1/∞ for an infinitesimal. John Wallis was a contemporary of Newton and one of the greatest intellectuals of the early renaissance of mathematics.