 W
WIn mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.
 W
WIn mathematics, specifically in incidence geometry and especially in projective geometry, a complete quadrangle is a system of geometric objects consisting of any four points in a plane, no three of which are on a common line, and of the six lines connecting the six pairs of points. Dually, a complete quadrilateral is a system of four lines, no three of which pass through the same point, and the six points of intersection of these lines. The complete quadrangle was called a tetrastigm by Lachlan (1893), and the complete quadrilateral was called a tetragram; those terms are occasionally still used.
 W
WIn mathematics, the Cremona–Richmond configuration is a configuration of 15 lines and 15 points, having 3 points on each line and 3 lines through each point, and containing no triangles. It was studied by Cremona (1877) and Richmond (1900). It is a generalized quadrangle with parameters (2,2). Its Levi graph is the Tutte–Coxeter graph.
 W
WIn geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues, and closely related to Desargues' theorem, which proves the existence of the configuration.
 W
WIn finite geometry, the Fano plane is the finite projective plane of order 2. It is the finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2) where PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.
 W
WIn the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive.
 W
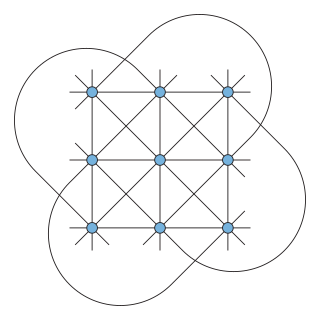
WIn geometry, the Grünbaum–Rigby configuration is a symmetric configuration consisting of 21 points and 21 lines, with four points on each line and four lines through each point. Originally studied by Felix Klein in the complex projective plane in connection with the Klein quartic, it was first realized in the Euclidean plane by Branko Grünbaum and John F. Rigby.
 W
WIn geometry, the Hesse configuration, introduced by Colin Maclaurin and studied by Hesse (1844), is a configuration of 9 points and 12 lines with three points per line and four lines through each point. It can be realized in the complex projective plane as the set of inflection points of an elliptic curve, but it has no realization in the Euclidean plane.
 W
WIn combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.
 W
WIn geometry, the Miquel configuration is a configuration of eight points and six circles in the Euclidean plane, with four points per circle and three circles through each point. Its Levi graph is the Rhombic dodecahedral graph. The configuration is related to Miquel's theorem.
 W
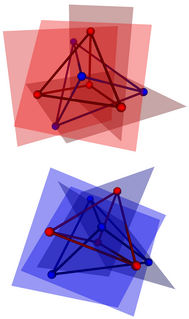
WIn geometry, the Möbius configuration or Möbius tetrads is a certain configuration in Euclidean space or projective space, consisting of two mutually inscribed tetrahedra: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa. Thus, for the resulting system of eight points and eight planes, each point lies on four planes, and each plane contains four points.
 W
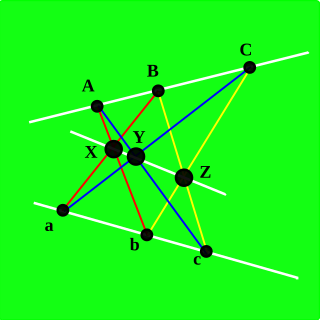
WIn geometry, the Möbius–Kantor configuration is a configuration consisting of eight points and eight lines, with three points on each line and three lines through each point. It is not possible to draw points and lines having this pattern of incidences in the Euclidean plane, but it is possible in the complex projective plane.
 W
WIn geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point.
 W
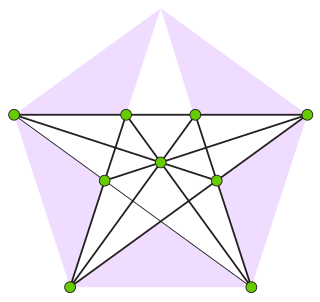
WIn geometry, the Perles configuration is a configuration of 9 points and 9 lines that can be realized in the Euclidean plane but for which every realization has at least one irrational number as one of its coordinates. It is not a projective configuration, however, because its points and lines do not all have the same number of incidences as each other. It was introduced by Micha Perles in the 1960s.
 W
WIn mathematics, the Reye configuration, introduced by Theodor Reye (1882), is a configuration of 12 points and 16 lines. Each point of the configuration belongs to four lines, and each line contains three points. Therefore, in the notation of configurations, the Reye configuration is written as 124163.
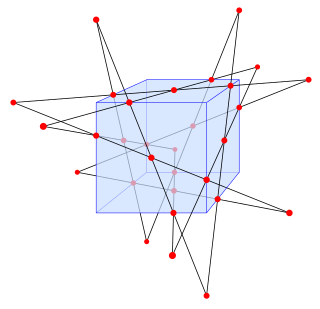 W
WIn geometry, the Schläfli double six is a configuration of 30 points and 12 lines, introduced by Schläfli (1858, p.115). The lines of the configuration can be partitioned into two subsets of six lines: each line is disjoint from (skew with) the lines in its own subset of six lines, and intersects all but one of the lines in the other subset of six lines. Each of the 12 lines of the configuration contains five intersection points, and each of these 30 intersection points belongs to exactly two lines, one from each subset, so in the notation of configurations the Schläfli double six is written 125302.
 W
WIn the mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage or Cremona–Richmond graph is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth 8 it is a cage and a Moore graph. It is bipartite, and can be constructed as the Levi graph of the generalized quadrangle W2. The graph is named after William Thomas Tutte and H. S. M. Coxeter; it was discovered by Tutte (1947) but its connection to geometric configurations was investigated by both authors in a pair of jointly published papers.