W

In geometry, a tiling is a partition of the plane into closed sets, without gaps or overlaps. A tiling is considered periodic if there exist translations in two independent directions which map the tiling onto itself. Such a tiling is composed of a single fundamental unit or primitive cell which repeats endlessly and regularly in two independent directions. An example of such a tiling is shown in the adjacent diagram. A tiling that cannot be constructed from a single primitive cell is called nonperiodic. If a given set of tiles allows only nonperiodic tilings, then this set of tiles is called aperiodic. The tilings obtained from an aperiodic set of tiles are often called aperiodic tilings, though strictly speaking it is the tiles themselves that are aperiodic.

W

This is a list of artists who actively explored mathematics in their artworks. Art forms practised by these artists include painting, sculpture, architecture, textiles and origami.

W

The following tables list the computational complexity of various algorithms for common mathematical operations.

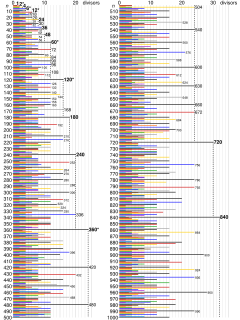
W

The tables below list all of the divisors of the numbers 1 to 1000.

W

This is a list of geometry topics, by Wikipedia page.Geometric shape covers standard terms for plane shapes

W

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

W

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.

W

The first of the International Mathematical Olympiads (IMOs) was held in Romania in 1959. The oldest of the International Science Olympiads, the IMO has since been held annually, except in 1980. That year, the competition initially planned to be held in Mongolia was cancelled due to the Soviet invasion of Afghanistan. Because the competition was initially founded for Eastern European countries participating in the Warsaw Pact, under the influence of the Eastern Bloc, the earlier IMOs were hosted only in Eastern European countries, gradually spreading to other nations. Sources differ about the cities hosting some of the early IMOs and the exact dates when they took place.

W

This article contains a list of mathematical knots and links. See also list of knots, list of geometric topology topics.

W

This article gives a table of some common Lie groups and their associated Lie algebras.

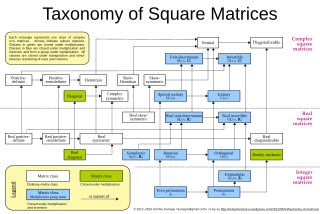
W

This page lists some important classes of matrices used in mathematics, science and engineering. A matrix is a rectangular array of numbers called entries. Matrices have a long history of both study and application, leading to diverse ways of classifying matrices. A first group is matrices satisfying concrete conditions of the entries, including constant matrices. Important examples include the identity matrix given by

W

In geometry, a polygon is traditionally a plane figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed chain. These segments are called its edges or sides, and the points where two of the edges meet are the polygon's vertices or corners.

W

This is a list of important publications in mathematics, organized by field.

W

The packing constant of a geometric body is the largest average density achieved by packing arrangements of congruent copies of the body. For most bodies the value of the packing constant is unknown. The following is a list of bodies in Euclidean spaces whose packing constant is known. Fejes Tóth proved that in the plane, a point symmetric body has a packing constant that is equal to its translative packing constant and its lattice packing constant. Therefore, any such body for which the lattice packing constant was previously known, such as any ellipse, consequently has a known packing constant. In addition to these bodies, the packing constants of hyperspheres in 8 and 24 dimensions are almost exactly known.

W

In mathematics, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle.

W

This table shows the 11 convex uniform tilings of the Euclidean plane, and their dual tilings.

W

Since the Renaissance, every century has seen the solution of more mathematical problems than the century before, yet many mathematical problems, both major and minor, still remain unsolved. These unsolved problems occur in multiple domains, including physics, computer science, algebra, analysis, combinatorics, algebraic, differential, discrete and Euclidean geometries, graph, group, model, number, set and Ramsey theories, dynamical systems, partial differential equations, and more. Some problems may belong to more than one discipline of mathematics and be studied using techniques from different areas. Prizes are often awarded for the solution to a long-standing problem, and lists of unsolved problems receive considerable attention.