17 Polyhedral stellation

In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram. That is, every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron, or inside of it.

This polyhedron can be seen as either a polyhedral stellation or a compound.

In geometry, this polyhedron can be seen as either a polyhedral stellation or a compound.

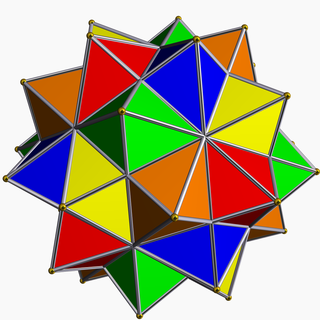
The compound of five cubes is one of the five regular polyhedral compounds. This compound was first described by Edmund Hess in 1876.

The compound of five octahedra is one of the five regular polyhedron compounds. This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876. It is unique among the regular compounds for not having a regular convex hull.

The compound of five tetrahedra is one of the five regular polyhedral compounds. This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.

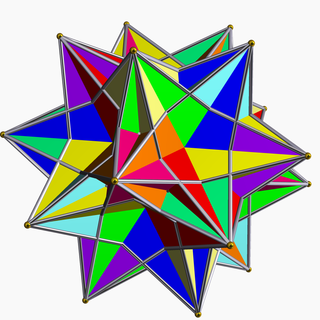
There are two different compounds of great icosahedron and great stellated dodecahedron: one is a dual compound and a stellation of the great icosidodecahedron, the other is a stellation of the icosidodecahedron.

The compound of ten tetrahedra is one of the five regular polyhedral compounds. This polyhedron can be seen as either a stellation of the icosahedron or a compound. This compound was first described by Edmund Hess in 1876.

In geometry, the excavated dodecahedron is a star polyhedron that looks like a dodecahedron with concave pentagonal pyramids in place of its faces. Its exterior surface represents the Ef1g1 stellation of the icosahedron. It appears in Magnus Wenninger's book Polyhedron Models as model 28, the third stellation of icosahedron.

The Fifty-Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates certain stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller.

In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces, with five pentagons meeting at each vertex, intersecting each other making a pentagrammic path.

In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter–Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.

In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.

In geometry, the great triambic icosahedron and medial triambic icosahedron (or midly triambic icosahedron) are visually identical dual uniform polyhedra. The exterior surface also represents the De2f2 stellation of the icosahedron. These figures can be differentiated by marking which intersections between edges are true vertices and which are not. In the above images, true vertices are marked by gold spheres, which can be seen in the concave Y-shaped areas. Alternatively, if the faces are filled with the even–odd rule, the internal structure of both shapes will differ.

In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.

In geometry, the small triambic icosahedron is a star polyhedron composed of 20 intersecting non-regular hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8. It is an isohedron, meaning that all of its faces are symmetric to each other, and Branko Grünbaum has conjectured that it is the only Euclidean isohedron with faces of six or more sides.

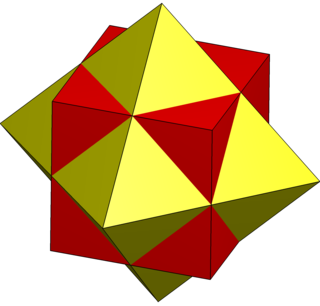
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula, a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's De Divina Proportione, 1509.