17 Trees (graph theory)

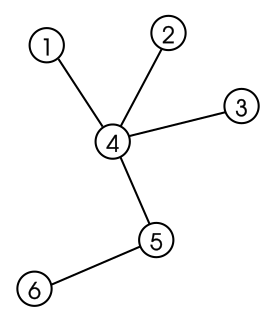
In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.

A Bethe lattice, introduced by Hans Bethe in 1935, is an infinite connected cycle-free graph where the vertices all have the same valence. I.e., each node is connected to z neighbours; z is called the coordination number. With one node chosen as root, all other nodes are seen to be arranged in shells around this root node, which is then also called the origin of the lattice. The number of nodes in the kth shell is given by

In graph theory, a branch of combinatorial mathematics, a block graph or clique tree is a type of undirected graph in which every biconnected component (block) is a clique.

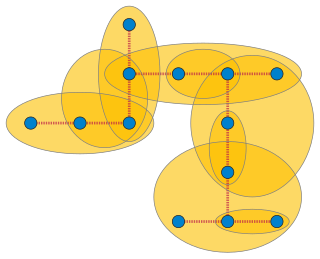
In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

In graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices are within distance 1 of a central path.

In mathematics, Cayley's formula is a result in graph theory named after Arthur Cayley. It states that for every positive integer , the number of trees on labeled vertices is .

In discrete mathematics, a centered tree is a tree with only one center, and a bicentered tree is a tree with two centers.

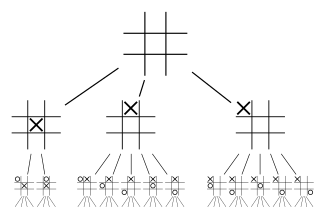
In game theory, a game tree is a directed graph whose nodes are positions in a game and whose edges are moves. The complete game tree for a game is the game tree starting at the initial position and containing all possible moves from each position; the complete tree is the same tree as that obtained from the extensive-form game representation.

In mathematics, a hypergraph H is called a hypertree if it admits a host graph T such that T is a tree. In other words, H is a hypertree if there exists a tree T such that every hyperedge of H is the set of vertices of a connected subtree of T. Hypertrees have also been called arboreal hypergraphs or tree hypergraphs.

In graph theory, a k-tree is an undirected graph formed by starting with a (k + 1)-vertex complete graph and then repeatedly adding vertices in such a way that each added vertex v has exactly k neighbors U such that, together, the k + 1 vertices formed by v and U form a clique.

In graph theory, an m-ary tree is a rooted tree in which each node has no more than m children. A binary tree is the special case where m = 2, and a ternary tree is another case with m = 3 that limits its children to three.

In mathematics, and more specifically in graph theory, a polytree is a directed acyclic graph whose underlying undirected graph is a tree. In other words, if we replace its directed edges with undirected edges, we obtain an undirected graph that is both connected and acyclic.

In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves. Alternatively, some authors define Sk to be the tree of order k with maximum diameter 2; in which case a star of k > 2 has k − 1 leaves.

The Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.

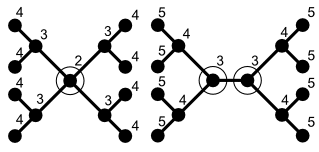
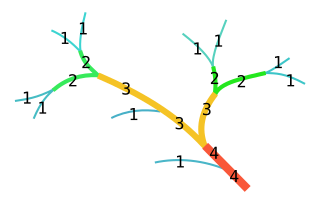
In mathematics, the Strahler number or Horton–Strahler number of a mathematical tree is a numerical measure of its branching complexity.

In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to define the treewidth of the graph and speed up solving certain computational problems on the graph.

In mathematics and computer science, an unrooted binary tree is an unrooted tree in which each vertex has either one or three neighbors.