18 Coordinate systems

In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the x-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and vice versa; this is the basis of analytic geometry.

In common usage, the abscissa refers to the horizontal (x) axis and the ordinate refers to the vertical (y) axis of a standard two-dimensional graph.

In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex. The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.

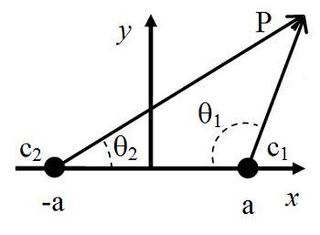
In mathematics, biangular coordinates are a coordinate system for the plane where and are two fixed points, and the position of a point P not on the line is determined by the angles and .

In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name curvilinear coordinates, coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved.

A geodetic datum or geodetic system is a system for precisely measuring locations on Earth or other planetary body. Datums are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A Horizontal datum is used to measure a location across the Earth's surface, in latitude and longitude or another coordinate system; a vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). Since the rise of the global positioning system (GPS), the ellipsoid and datum WGS 84 it uses has supplanted most others in many applications. The WGS 84 is intended for global use, unlike most earlier datums.

In mathematics, hyperbolic coordinates are a method of locating points in quadrant I of the Cartesian plane :\ x>0,\ y>0\ \}=Q} .

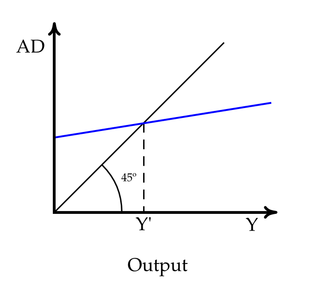
In a 2-dimensional Cartesian coordinate system, with x representing the abscissa and y the ordinate, the identity line or line of equality is the y = x line. The line, sometimes called the 1:1 line, has a slope of 1. When the abscissa and ordinate are on the same scale, the identity line forms a 45° angle with the abscissa, and is thus also, informally, called the 45° line. The line is often used as a reference in a 2-dimensional scatter plot comparing two sets of data expected to be identical under ideal conditions. When the corresponding data points from the two data sets are equal to each other, the corresponding scatters fall exactly on the identity line.

In the theory of many-particle systems, Jacobi coordinates often are used to simplify the mathematical formulation. These coordinates are particularly common in treating polyatomic molecules and chemical reactions, and in celestial mechanics. An algorithm for generating the Jacobi coordinates for N bodies may be based upon binary trees. In words, the algorithm is described as follows:Let mj and mk be the masses of two bodies that are replaced by a new body of virtual mass M = mj + mk. The position coordinates xj and xk are replaced by their relative position rjk = xj − xk and by the vector to their center of mass Rjk = /(mj + mk). The node in the binary tree corresponding to the virtual body has mj as its right child and mk as its left child. The order of children indicates the relative coordinate points from xk to xj. Repeat the above step for N − 1 bodies, that is, the N − 2 original bodies plus the new virtual body.

In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. The radial coordinate is often denoted by r or ρ, and the angular coordinate by φ, θ, or t. Angles in polar notation are generally expressed in either degrees or radians.

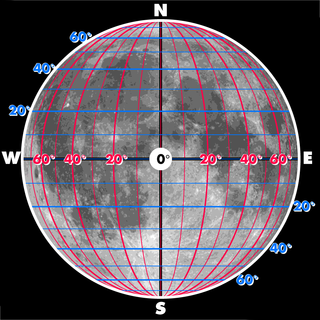
Selenographic coordinates are used to refer to locations on the surface of Earth's moon. Any position on the lunar surface can be referenced by specifying two numerical values, which are comparable to the latitude and longitude of Earth. The longitude gives the position east or west of the Moon's prime meridian, which is the line passing from the lunar north pole through the point on the lunar surface directly facing Earth to the lunar south pole. This can be thought of as the midpoint of the visible Moon as seen from the Earth. The latitude gives the position north or south of the lunar equator. Both of these coordinates are given in degrees.

The terms toroidal and poloidal refer to directions relative to a torus of reference. The poloidal direction follows a small circular ring around the surface, while the toroidal direction follows a large circular ring around the torus, encircling the central void.

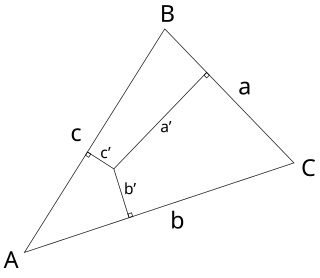
In geometry, the trilinear coordinates x:y:z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x:y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y:z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z:x and vertices C and A.

In mathematics, two-center bipolar coordinates is a coordinate system, based on two coordinates which give distances from two fixed centers, and . This system is very useful in some scientific applications.

Note: This page uses common physics notation for spherical coordinates, in which is the angle between the z axis and the radius vector connecting the origin to the point in question, while is the angle between the projection of the radius vector onto the x-y plane and the x axis. Several other definitions are in use, and so care must be taken in comparing different sources.

In theoretical physics, the composition of two non-collinear Lorentz boosts results in a Lorentz transformation that is not a pure boost but is the composition of a boost and a rotation. This rotation is called Thomas rotation, Thomas–Wigner rotation or Wigner rotation. The rotation was discovered by Llewellyn Thomas in 1926, and derived by Wigner in 1939. If a sequence of non-collinear boosts returns an object to its initial velocity, then the sequence of Wigner rotations can combine to produce a net rotation called the Thomas precession.

The World Geodetic System (WGS) is a standard for use in cartography, geodesy, and satellite navigation including GPS. This standard includes the definition of the coordinate system's fundamental and derived constants, the ellipsoidal (normal) Earth Gravitational Model (EGM), a description of the associated World Magnetic Model (WMM), and a current list of local datum transformations.