19 Analytic number theory

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.

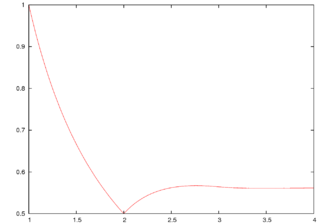
The Buchstab function is the unique continuous function :\mathbb {R} _{\geq 1}\rightarrow \mathbb {R} _{>0}} defined by the delay differential equation

In analytic number theory, the Dickman function or Dickman–de Bruijn function ρ is a special function used to estimate the proportion of smooth numbers up to a given bound. It was first studied by actuary Karl Dickman, who defined it in his only mathematical publication, and later studied by the Dutch mathematician Nicolaas Govert de Bruijn.

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. Every elliptic curve over a field of characteristic different from 2 and 3 can be described as a plane algebraic curve given by an equation of the form

Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even whole number greater than 2 is the sum of two prime numbers.

In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states thatEvery odd number greater than 5 can be expressed as the sum of three primes.

In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form

Legendre's constant is a mathematical constant occurring in a formula conjectured by Adrien-Marie Legendre to capture the asymptotic behavior of the prime-counting function . Its value is now known to be exactly 1.

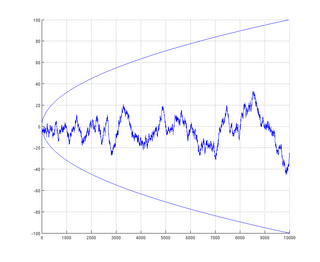
In mathematics, the Mertens conjecture is the statement that the Mertens function is bounded by . Although now disproven, it has been shown to imply the Riemann hypothesis. It was conjectured by Thomas Joannes Stieltjes, in an 1885 letter to Charles Hermite, and again in print by Franz Mertens (1897), and disproved by Andrew Odlyzko and Herman te Riele (1985). It is a striking example of a mathematical conjecture proven false despite a large amount of computational evidence in its favor.

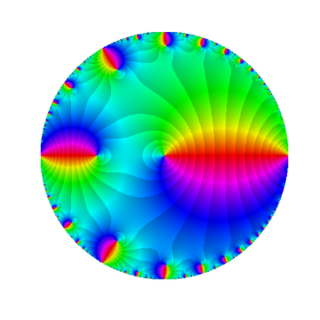
In mathematics, the modular group is the projective special linear group PSL(2, Z) of 2 × 2 matrices with integer coefficients and unit determinant. The matrices A and −A are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic.

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery (1973) that the pair correlation between pairs of zeros of the Riemann zeta function is

The Music of the Primes is a 2003 book by Marcus du Sautoy, a professor in mathematics at the University of Oxford, on the history of prime number theory. In particular he examines the Riemann hypothesis, the proof of which would revolutionize our understanding of prime numbers. He traces the prime number theorem back through history, highlighting the work of some of the greatest mathematical minds along the way.

"Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" is a seminal 9-page paper by Bernhard Riemann published in the November 1859 edition of the Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin.

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x).

In mathematics, the Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.

The Riemann zeta function or Euler–Riemann zeta function, ζ(s), is a function of a complex variable s that analytically continues the sum of the Dirichlet series

In number theory, the second Hardy–Littlewood conjecture concerns the number of primes in intervals. Along with the first Hardy–Littlewood conjecture, the second Hardy–Littlewood conjecture was proposed by G. H. Hardy and John Edensor Littlewood in 1923.

In mathematics, Stirling's approximation is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of n. It is named after James Stirling, though it was first stated by Abraham de Moivre.