19 Integral calculus

In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function f is a differentiable function F whose derivative is equal to the original function f. This can be stated symbolically as F' = f. The process of solving for antiderivatives is called antidifferentiation, and its opposite operation is called differentiation, which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as F and G.

Arc length is the distance between two points along a section of a curve.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:

Disc integration, also known in integral calculus as the disc method, is a method for calculating the volume of a solid of revolution of a solid-state material when integrating along an axis "parallel" to the axis of revolution. This method models the resulting three-dimensional shape as a stack of an infinite number of discs of varying radius and infinitesimal thickness. It is also possible to use the same principles with rings instead of discs to obtain hollow solids of revolutions. This is in contrast to shell integration, which integrates along an axis perpendicular to the axis of revolution.

The Fresnel integrals S(x) and C(x) are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function. They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations:

In mathematics, a hyperbolic angle is a geometric figure that defines a hyperbolic sector. The relationship of a hyperbolic angle to a hyperbola parallels the relationship of an "ordinary" angle to a circle.

A hyperbolic sector is a region of the Cartesian plane {(x,y)} bounded by rays from the origin to two points and and by the rectangular hyperbola xy = 1.

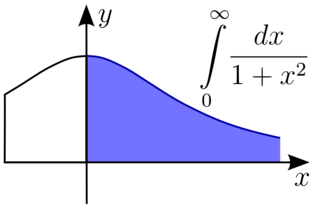
In mathematical analysis, an improper integral is the limit of a definite integral as an endpoint of the interval(s) of integration approaches either a specified real number, , , or in some instances as both endpoints approach limits. Such an integral is often written symbolically just like a standard definite integral, in some cases with infinity as a limit of integration.

In mathematics, an indicator function or a characteristic function is a function defined on a set X that indicates membership of an element in a subset A of X, having the value 1 for all elements of A and the value 0 for all elements of X not in A. It is usually denoted by a symbol 1 or I, sometimes in boldface or blackboard boldface, with a subscript specifying the subset.

In mathematics, the integral test for convergence is a method used to test infinite series of non-negative terms for convergence. It was developed by Colin Maclaurin and Augustin-Louis Cauchy and is sometimes known as the Maclaurin–Cauchy test.

In mathematics, particularly in integral calculus, the localization theorem allows, under certain conditions, to infer the nullity of a function given only information about its continuity and the value of its integral.

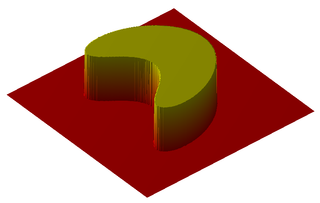
In mathematics, a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in are called double integrals, and integrals of a function of three variables over a region in are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.

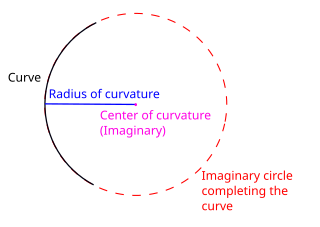
In differential geometry, the radius of curvature, R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.

In mathematics, a Riemann sum is a certain kind of approximation of an integral by a finite sum. It is named after nineteenth century German mathematician Bernhard Riemann. One very common application is approximating the area of functions or lines on a graph, but also the length of curves and other approximations.

Shell integration is a method for calculating the volume of a solid of revolution, when integrating along an axis perpendicular to the axis of revolution. This is in contrast to disc integration which integrates along the axis parallel to the axis of revolution.

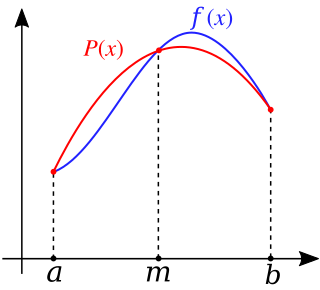
In numerical integration, Simpson's rules are several approximations for definite integrals, named after Thomas Simpson (1710–1761).

In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane.

A surface of revolution is a surface in Euclidean space created by rotating a curve around an axis of rotation.

In mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions. In calculus, trigonometric substitution is a technique for evaluating integrals. Moreover, one may use the trigonometric identities to simplify certain integrals containing radical expressions. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.