 W
WIn mathematics, particularly in algebraic geometry, complex analysis and algebraic number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions. Abelian varieties are at the same time among the most studied objects in algebraic geometry and indispensable tools for much research on other topics in algebraic geometry and number theory.
 W
WIn algebraic geometry, a Barth surface is one of the complex nodal surfaces in 3 dimensions with large numbers of double points found by Wolf Barth (1996). Two examples are the Barth sextic of degree 6 with 65 double points, and the Barth decic of degree 10 with 345 double points.
 W
WIn algebraic geometry, the Cayley surface, named after Arthur Cayley, is a cubic nodal surface in 3-dimensional projective space with four conical points. It can be given by the equation
 W
WIn algebraic geometry, a Châtelet surface is a rational surface studied by Châtelet (1959) given by an equation
 W
WIn mathematics, the Clebsch diagonal cubic surface, or Klein's icosahedral cubic surface, is a non-singular cubic surface, studied by Clebsch (1871) and Klein (1873), all of whose 27 exceptional lines can be defined over the real numbers. The term Klein's icosahedral surface can refer to either this surface or its blowup at the 10 Eckardt points.
 W
WIn geometry, a (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex. Each of those lines is called a generatrix of the surface.
 W
WIn mathematics, a cubic surface is a surface in 3-dimensional space defined by one polynomial equation of degree 3. Cubic surfaces are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space, and so cubic surfaces are generally considered in projective 3-space . The theory also becomes more uniform by focusing on surfaces over the complex numbers rather than the real numbers; note that a complex surface has real dimension 4. A simple example is the Fermat cubic surface
 W
WIn algebraic geometry, an Endrass surface is a nodal surface of degree 8 with 168 real nodes, found by Stephan Endrass (1997). As of 2007, it remained the record-holder for the most number of real nodes for its degree; however, the best proven upper bound, 174, does not match the lower bound given by this surface.
 W
WIn differential geometry and algebraic geometry, the Enneper surface is a self-intersecting surface that can be described parametrically by:
 W
WIn geometry, the Fermat cubic, named after Pierre de Fermat, is a surface defined by
 W
WIn mathematics, a complex analytic K3 surface is a compact connected complex manifold of dimension 2 with trivial canonical bundle and irregularity zero. An (algebraic) K3 surface over any field means a smooth proper geometrically connected algebraic surface that satisfies the same conditions. In the Enriques–Kodaira classification of surfaces, K3 surfaces form one of the four classes of minimal surfaces of Kodaira dimension zero. A simple example is the Fermat quartic surface
 W
WIn algebraic geometry, a Kummer quartic surface, first studied by Ernst Kummer (1864), is an irreducible nodal surface of degree 4 in with the maximal possible number of 16 double points. Any such surface is the Kummer variety of the Jacobian variety of a smooth hyperelliptic curve of genus 2; i.e. a quotient of the Jacobian by the Kummer involution x ↦ −x. The Kummer involution has 16 fixed points: the 16 2-torsion point of the Jacobian, and they are the 16 singular points of the quartic surface. Resolving the 16 double points of the quotient of a torus by the Kummer involution gives a K3 surface with 16 disjoint rational curves; these K3 surfaces are also sometimes called Kummer surfaces.
 W
WIn mathematics, the Labs septic surface is a degree-7 (septic) nodal surface with 99 nodes found by Labs (2006). As of 2015, it has the largest known number of nodes of a degree-7 surface, though this number is still less than the best known upper bound of 104 nodes given by Giventalʹ (1983) and Varchenko (1983).
 W
WIn mathematics, the Peano surface is the graph of the two-variable function
 W
WIn geometry, a pinch point or cuspidal point is a type of singular point on an algebraic surface.
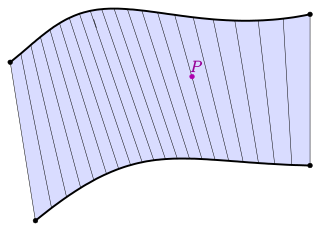 W
WIn geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.
 W
WIn algebraic geometry, a Sarti surface is a degree-12 nodal surface with 600 nodes, found by Alessandra Sarti (2008). The maximal possible number of nodes of a degree-12 surface is not known, though Yoichi Miyaoka showed that it is at most 645.
 W
WIn algebraic geometry, a tetrahedroid is a special kind of Kummer surface studied by Cayley (1846), with the property that the intersections with the faces of a fixed tetrahedron are given by two conics intersecting in four nodes. Tetrahedroids generalize Fresnel's wave surface.
 W
WIn algebraic geometry, a Togliatti surface is a nodal surface of degree five with 31 nodes. The first examples were constructed by Eugenio G. Togliatti (1940). Arnaud Beauville (1980) proved that 31 is the maximum possible number of nodes for a surface of this degree, showing this example to be optimal.
 W
WIn mathematics, Fresnel's wave surface, found by Augustin-Jean Fresnel in 1822, is a quartic surface describing the propagation of light in an optically biaxial crystal. Wave surfaces are special cases of tetrahedroids which are in turn special cases of Kummer surfaces.