 W
WIn mathematics, a bijection, bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements. In mathematical terms, a bijective function f: X → Y is a one-to-one (injective) and onto (surjective) mapping of a set X to a set Y. The term one-to-one correspondence must not be confused with one-to-one function.
 W
WIn mathematics, injections, surjections and bijections are classes of functions distinguished by the manner in which arguments and images are related or mapped to each other.
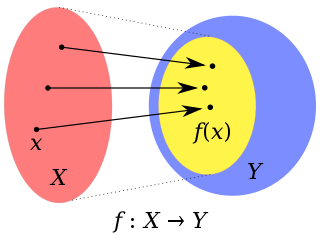 W
WIn mathematics, the codomain or set of destination of a function is the set into which all of the output of the function is constrained to fall. It is the set Y in the notation f: X → Y. The term range is sometimes ambiguously used to refer to either the codomain or image of a function.
 W
WIn mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, two disjoint sets are sets whose intersection is the empty set. For example, {1, 2, 3} and {4, 5, 6} are disjoint sets, while {1, 2, 3} and {3, 4, 5} are not disjoint. A collection of more than two sets is called disjoint if any two distinct sets of the collection are disjoint.
 W
WIn mathematics, the domain or set of departure of a function is the set into which all of the input of the function is constrained to fall. It is the set X in the notation f: X → Y, and is alternatively denoted as . Since a function is defined on its entire domain, its domain coincides with its domain of definition. However, this coincidence is no longer true for a partial function, since the domain of definition of a partial function can be a proper subset of the domain.
 W
WIn mathematics, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories ensure that the empty set exists by including an axiom of empty set, while in other theories, its existence can be deduced. Many possible properties of sets are vacuously true for the empty set.
 W
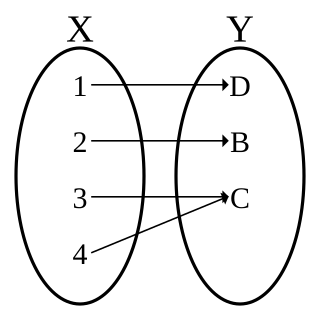
WIn mathematics, a function is a binary relation between two sets that associates every element of the first set to exactly one element of the second set. Typical examples are functions from integers to integers, or from the real numbers to real numbers.
 W
WIn mathematics, an identity function, also called an identity relation or identity map or identity transformation, is a function that always returns the same value that was used as its argument. That is, for f being identity, the equality f(x) = x holds for all x.
 W
WIn mathematics, the image of a function is the set of all output values it may produce.
 W
WIn mathematics, if A is a subset of B, then the inclusion map is the function ι that sends each element x of A to x, treated as an element of B:
 W
WIn mathematics, an indicator function or a characteristic function is a function defined on a set X that indicates membership of an element in a subset A of X, having the value 1 for all elements of A and the value 0 for all elements of X not in A. It is usually denoted by a symbol 1 or I, sometimes in boldface or blackboard boldface, with a subscript specifying the subset.
 W
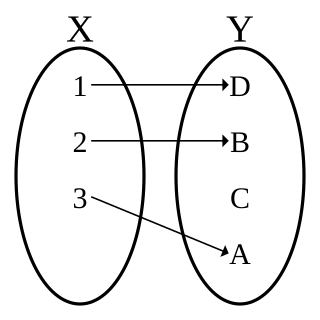
WIn mathematics, an injective function is a function that maps distinct elements of its domain to distinct elements of its codomain. In other words, every element of the function's codomain is the image of at most one element of its domain. The term one-to-one function must not be confused with one-to-one correspondence that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain.
 W
WIn mathematics, the intersection of two sets A and B, denoted by A ∩ B, is the set containing all elements of A that also belong to B.
 W
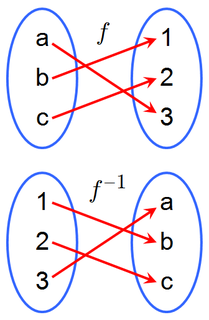
WIn mathematics, an inverse function is a function that "reverses" another function: if the function f applied to an input x gives a result of y, then applying its inverse function g to y gives the result x, i.e., g(y) = x if and only if f(x) = y. The inverse function of f is also denoted as .
 W
WA k-cell is a higher-dimensional version of a rectangle or rectangular solid. It is the Cartesian product of k closed intervals on the real line. This means that a k-dimensional rectangular solid has each of its edges equal to one of the closed intervals used in the definition. The k intervals need not be identical. For example, a 2-cell is a rectangle in R2 such that the sides of the rectangles are parallel to the coordinate axes.
 W
WIn mathematics, a map is often used as a synonym for a function, but may also refer to some generalizations. Originally, this was an abbreviation of mapping, which often refers to the action of applying a function to the elements of its domain. This terminology is not completely fixed, as these terms are generally not formally defined, and can be considered to be jargon. These terms may have originated as a generalization of the process of making a geographical map, which consists of mapping the Earth surface to a sheet of paper.
 W
WIn mathematics, a partition of a set is a grouping of its elements into non-empty subsets, in such a way that every element is included in exactly one subset.
 W
WIn mathematics, the range of a function may refer to either of two closely related concepts:The codomain of the function The image of the function
 W
WIn mathematics, a set A is a subset of a set B if all elements of A are also elements of B; B is then a superset of A. It is possible for A and B to be equal; if they are unequal, then A is a proper subset of B. The relationship of one set being a subset of another is called inclusion. A is a subset of B may also be expressed as B includes A or A is included in B.
 W
WIn mathematics, a function f from a set X to a set Y is surjective, if for every element y in the codomain Y of f, there is at least one element x in the domain X of f such that f(x) = y. It is not required that x be unique; the function f may map one or more elements of X to the same element of Y.