20 Combinatorics stubs

In graph theory, an Andrásfai graph is a triangle-free circulant graph named after Béla Andrásfai.

In the mathematical domain of graph theory, a bidirected graph is a graph in which each edge is given an independent orientation at each end. Thus, there are three kinds of bidirected edges: those where the arrows point outward, towards the vertices, at both ends; those where both arrows point inward, away from the vertices; and those in which one arrow points away from its vertex and towards the opposite end, while the other arrow points in the same direction as the first, away from the opposite end and towards its own vertex.

In mathematics, the cake number, denoted by Cn, is the maximum number of regions into which a 3-dimensional cube can be partitioned by exactly n planes. The cake number is so-called because one may imagine each partition of the cube by a plane as a slice made by a knife through a cube-shaped cake.

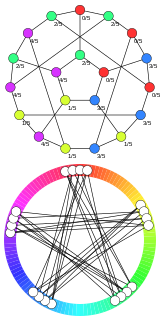
In graph theory, circular coloring may be viewed as a refinement of usual graph coloring. The circular chromatic number of a graph , denoted can be given by any of the following definitions, all of which are equivalent. is the infimum over all real numbers so that there exists a map from to a circle of circumference 1 with the property that any two adjacent vertices map to points at distance along this circle. is the infimum over all rational numbers so that there exists a map from to the cyclic group with the property that adjacent vertices map to elements at distance apart. In an oriented graph, declare the imbalance of a cycle to be divided by the minimum of the number of edges directed clockwise and the number of edges directed counterclockwise. Define the imbalance of the oriented graph to be the maximum imbalance of a cycle. Now, is the minimum imbalance of an orientation of .

In metric graph theory, a convex subgraph of an undirected graph G is a subgraph that includes every shortest path in G between two of its vertices. Thus, it is analogous to the definition of a convex set in geometry, a set that contains the line segment between every pair of its points.

In digital geometry, a cutting sequence is a sequence of symbols whose elements correspond to the individual grid lines crossed ("cut") as a curve crosses a square grid.

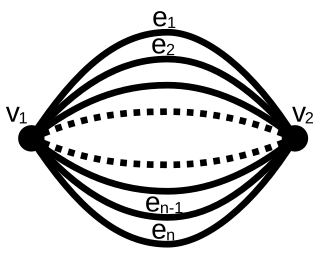
In graph theory, a dipole graph is a multigraph consisting of two vertices connected with a number of parallel edges. A dipole graph containing n edges is called the order-n dipole graph, and is denoted by Dn. The order-n dipole graph is dual to the cycle graph Cn.

In the mathematical field of graph theory, the double-star snark is a snark with 30 vertices and 45 edges.

An edge-matching puzzle is a type of tiling puzzle involving tiling an area with polygons whose edges are distinguished with colours or patterns, in such a way that the edges of adjacent tiles match.

The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles.

In the mathematical field of graph theory, the Fritsch graph is a planar graph with 9 vertices and 21 edges. It was obtained by Fritsch as a minimal sized counterexample to the Alfred Kempe's attempt to prove the four-color theorem.

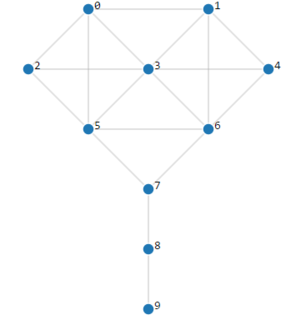
In graph theory, the Krackhardt kite graph is a simple graph with ten nodes. The graph is named after David Krackhardt, a researcher of social network theory.

L(2, 1)-coloring is a particular case of L(h, k)-coloring which is in fact a proper coloring. In L(2, 1)-coloring of a graph, G, the vertices of the graph G is colored or labelled in such a way that the adjacent vertices get labels that differ by at least two. Also the vertices that are at a distance of two from each other get labels that differ by at least one.

In the mathematical field of graph theory, the Livingstone graph is a distance-transitive graph with 266 vertices and 1463 edges. Its intersection array is {11,10,6,1;1,1,5,11}. It is the largest distance-transitive graph with degree 11.

In the mathematical discipline of graph theory, the (m,n)-lollipop graph is a special type of graph consisting of a complete graph (clique) on m vertices and a path graph on n vertices, connected with a bridge.

In the mathematical field of graph theory, a Platonic graph is a graph that has one of the Platonic solids as its skeleton. There are 5 Platonic graphs, and all of them are regular, polyhedral, and also Hamiltonian graphs.Tetrahedral graph – 4 vertices, 6 edges Octahedral graph – 6 vertices, 12 edges Cubical graph – 8 vertices, 12 edges Icosahedral graph – 12 vertices, 30 edges Dodecahedral graph – 20 vertices, 30 edges

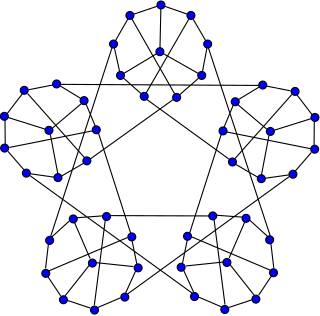
In the mathematical field of graph theory, the Szekeres snark is a snark with 50 vertices and 75 edges. It was the fifth known snark, discovered by George Szekeres in 1973.

In mathematics, Szymanski's conjecture, named after Ted H. Szymanski (1989), states that every permutation on the n-dimensional doubly directed hypercube graph can be routed with edge-disjoint paths. That is, if the permutation σ matches each vertex v to another vertex σ(v), then for each v there exists a path in the hypercube graph from v to σ(v) such that no two paths for two different vertices u and v use the same edge in the same direction.

A trellis is a graph whose nodes are ordered into vertical slices (time) with each node at each time connected to at least one node at an earlier and at least one node at a later time. The earliest and latest times in the trellis have only one node.

In the mathematical field of graph theory, the Watkins snark is a snark with 50 vertices and 75 edges. It was discovered by John J. Watkins in 1989.