20 Hexagonal tilings

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6}.

In geometry, the alternated order-4 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of (3,4,4), h{6,4}, and hr{6,6}.

In geometry, the cantic order-4 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{(4,4,3)} or h2{6,4}.

In the field of hyperbolic geometry, the hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere, a surface in hyperbolic space that approaches a single ideal point at infinity.

In 2-dimensional hyperbolic geometry, the infinite-order hexagonal tiling is a regular tiling. It has Schläfli symbol of {6,∞}. All vertices are ideal, located at "infinity", seen on the boundary of the Poincaré hyperbolic disk projection.

A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(p,q). Dihedra have also been called bihedra, flat polyhedra, or doubly covered polygons.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6}.

In the geometry of hyperbolic 3-space, the order-3-7 hexagonal honeycomb or a regular space-filling tessellation with Schläfli symbol {6,3,7}.

In geometry, the order-4 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,4}.

In the field of hyperbolic geometry, the order-4 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In geometry, the order-5 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,5}.

In the field of hyperbolic geometry, the order-5 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere, a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In geometry, the order-6 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,6} and is self-dual.

In the field of hyperbolic geometry, the order-6 hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells with an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In geometry, the order-8 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,8}.

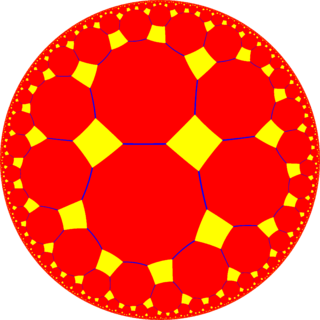
In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.

In geometry, the truncated order-4 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{6,4}. A secondary construction tr{6,6} is called a truncated hexahexagonal tiling with two colors of dodecagons.

In geometry, the truncated order-5 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{6,5}.

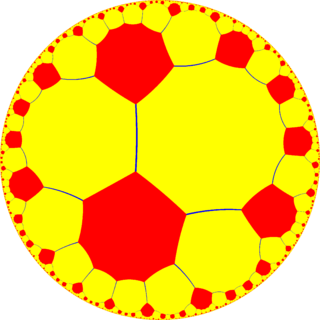
In geometry, the truncated order-6 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{6,6}. It can also be identically constructed as a cantic order-6 square tiling, h2{4,6}

In geometry, the truncated order-8 hexagonal tiling is a semiregular tiling of the hyperbolic plane. It has Schläfli symbol of t{6,8}.