20 Types of triangles

An acute triangle is a triangle with three acute angles. An obtuse triangle is a triangle with one obtuse angle and two acute angles. Since a triangle's angles must sum to 180° in Euclidean geometry, no Euclidean triangle can have more than one obtuse angle.

In plane geometry, an automedian triangle is a triangle in which the lengths of the three medians are proportional to the lengths of the three sides, in a different order. The three medians of an automedian triangle may be translated to form the sides of a second triangle that is similar to the first one.

The Calabi triangle is a special triangle found by Eugenio Calabi and defined by its property of having three different placements for the largest square that it contains. It is an obtuse isosceles triangle with an irrational but algebraic ratio between the lengths of its sides and its base.

In geometry, a circular triangle is a triangle with circular arc edges.

A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.

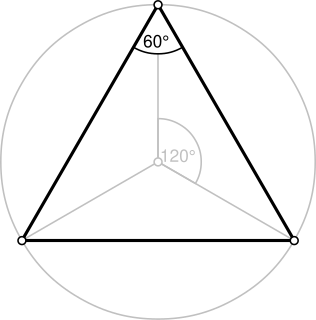
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

A golden triangle, also called a sublime triangle, is an isosceles triangle in which the duplicated side is in the golden ratio to the base side:

A heptagonal triangle is an obtuse scalene triangle whose vertices coincide with the first, second, and fourth vertices of a regular heptagon. Thus its sides coincide with one side and the adjacent shorter and longer diagonals of the regular heptagon. All heptagonal triangles are similar, and so they are collectively known as the heptagonal triangle. Its angles have measures and and it is the only triangle with angles in the ratios 1:2:4. The heptagonal triangle has various remarkable properties

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.

In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all are ideal points. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles. The vertices are sometimes called ideal vertices. All ideal triangles are congruent.

An integer triangle or integral triangle is a triangle all of whose sides have lengths that are integers. A rational triangle can be defined as one having all sides with rational length; any such rational triangle can be integrally rescaled to obtain an integer triangle, so there is no substantive difference between integer triangles and rational triangles in this sense. However, other definitions of the term "rational triangle" also exist: In 1914 Carmichael used the term in the sense that we today use the term Heronian triangle; Somos uses it to refer to triangles whose ratios of sides are rational; Conway and Guy define a rational triangle as one with rational sides and rational angles measured in degrees—in which case the only rational triangle is the rational-sided equilateral triangle.

In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.

A Kepler triangle is a right triangle with edge lengths in a geometric progression. The ratio of the progression is √φ, where φ is the golden ratio, and can be written: , or approximately 1 : 1.272 : 1.618. The squares of the edges of this triangle are also in geometric progression according to the golden ratio itself.

A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.

A Reuleaux triangle [ʁœlo] is a shape formed from the intersection of three circular disks, each having its center on the boundary of the other two. Its boundary is a curve of constant width, the simplest and best known such curve other than the circle itself. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because all its diameters are the same, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

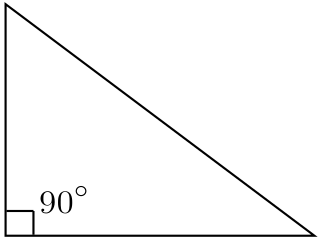
A right triangle or right-angled triangle is a triangle in which one angle is a right angle. The relation between the sides and angles of a right triangle is the basis for trigonometry.

A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.