20 Zonohedra

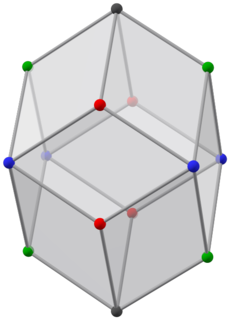
In geometry, the Bilinski dodecahedron is a 12-sided convex polyhedron with congruent rhombic faces. It has the same topology but different geometry from the face-transitive rhombic dodecahedron.

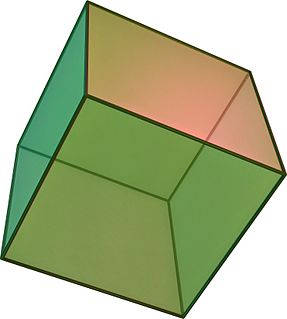
In geometry, a scientific cuboid cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.

In geometry, the decagonal prism is the eighth in the infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra. The decagonal prism has 12 faces, 30 edges, and 20 vertices. If faces are all regular, it is a semiregular or prismatic uniform polyhedron.

In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.

In geometry, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism.

In geometry, the hexagonal prism is a prism with hexagonal base. This polyhedron has 8 faces, 18 edges, and 12 vertices.

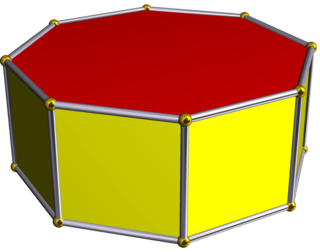
In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.

In geometry, a parallelepiped, parallelopiped or parallelopipedon is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—parallelepiped and cube in three dimensions, parallelogram and square in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only parallelograms and parallelepipeds exist. Three equivalent definitions of parallelepiped area polyhedron with six faces (hexahedron), each of which is a parallelogram, a hexahedron with three pairs of parallel faces, and a prism of which the base is a parallelogram.

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of two types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

A rhombic enneacontahedron is a polyhedron composed of 90 rhombic faces; with three, five, or six rhombi meeting at each vertex. It has 60 broad rhombi and 30 slim. The rhombic enneacontahedron is a zonohedron with a superficial resemblance to the rhombic triacontahedron.

In geometry, a rhombic hectotriadiohedron, rhombhectotriadiohedron or rhombic 132-hedron is a polyhedron composed of 132 rhombic faces. Rhombic faces have 5 positions within octahedral symmetry. There are two topological types, with the same number of elements, the same symmetry, but having a somewhat different arrangement of rhombic faces.

In geometry, a rhombic hexecontahedron is a stellation of the rhombic triacontahedron. It is nonconvex with 60 golden rhombic faces with icosahedral symmetry. It was described mathematically in 1940 by Helmut Unkelbach.

The rhombic icosahedron is a polyhedron shaped like an oblate sphere. Its 20 faces are congruent golden rhombi, of which three, four, or five meet at each vertex. It has 5 faces (green on the first figure) meeting at each of its 2 poles (these 2 vertices lie on its axis of (5-fold) symmetry), and 10 faces following its equator (2 of their 4 edges (each) lie on the equator polyline). It has D5d, [2+,10], (2*5) symmetry, order 20.

In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron.

In geometry, a rhombohedron is a three-dimensional figure like a cuboid, except that its faces are not rectangles but rhombi. It is a special case of a parallelepiped where all edges are the same length. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells.

A scutoid is a geometric solid between two parallel surfaces. The boundary of each of the surfaces is a polygon, and the vertices of the two end polygons are joined by either a curve or a Y-shaped connection on at least one of the edges, but not necessarily all of the edges. Scutoids present at least one vertex between these two planes. Scutoids are not necessarily convex, and lateral faces are not necessarily planar, so several scutoids can pack together to fill all the space between the two parallel surfaces. They may be more generally described as a mix between a frustum and a prismatoid.

In geometry, a trigonal trapezohedron, or trigonal deltohedron, or isohedral rhombohedron, or rhombic hexahedron is a three-dimensional figure formed by six congruent rhombi.

In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.

In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.