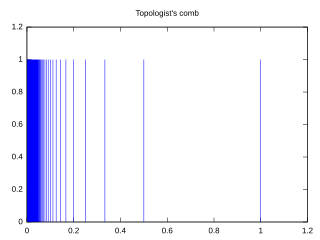
 W
WIn mathematics, particularly topology, a comb space is a particular subspace of that resembles a comb. The comb space has properties that serve as a number of counterexamples. The topologist's sine curve has similar properties to the comb space. The deleted comb space is a variation on the comb space.
 W
WIn mathematics, a cubical complex or cubical set is a set composed of points, line segments, squares, cubes, and their n-dimensional counterparts. They are used analogously to simplicial complexes and CW complexes in the computation of the homology of topological spaces.
 W
WIn geometric topology, the dogbone space, constructed by R. H. Bing (1957), is a quotient space of three-dimensional Euclidean space such that all inverse images of points are points or tame arcs, yet it is not homeomorphic to . The name "dogbone space" refers to a fanciful resemblance between some of the diagrams of genus 2 surfaces in R. H. Bing's paper and a dog bone. Bing (1959) showed that the product of the dogbone space with is homeomorphic to .
 W
WIn topology, the dunce hat is a compact topological space formed by taking a solid triangle and gluing all three sides together, with the orientation of one side reversed. Simply gluing two sides oriented in the same direction would yield a cone much like the dunce cap, but the gluing of the third side results in identifying the base of the cap with a line joining the base to the point.
 W
WEuclidean space is the fundamental space of classical geometry. Originally it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any nonnegative integer dimension, including the three-dimensional space and the Euclidean plane. It was introduced by the Ancient Greek mathematician Euclid of Alexandria, and the qualifier Euclidean is used to distinguish it from other spaces that were later discovered in physics and modern mathematics.
 W
WIn mathematics, the Hawaiian earring is the topological space defined by the union of circles in the Euclidean plane with center and radius for endowed with the subspace topology:
 W
WIn mathematics, a hedgehog space is a topological space consisting of a set of spines joined at a point.
 W
WIn mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology. Furthermore, many interesting topological spaces can be embedded in the Hilbert cube; that is, can be viewed as subspaces of the Hilbert cube.
 W
WIn mathematics, a hyperbolic space is a homogeneous space that has a constant negative curvature, where in this case the curvature is the sectional curvature. It is hyperbolic geometry in more than 2 dimensions, and is distinguished from Euclidean spaces with zero curvature that define the Euclidean geometry, and elliptic geometry that have a constant positive curvature.
 W
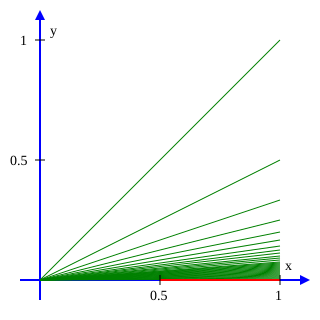
WIn topology, a branch of mathematics, the infinite broom is a subset of the Euclidean plane that is used as an example distinguishing various notions of connectedness. The closed infinite broom is the closure of the infinite broom, and is also referred to as the broom space.
 W
WIn topology, a branch of mathematics, the Knaster–Kuratowski fan is a specific connected topological space with the property that the removal of a single point makes it totally disconnected. It is also known as Cantor's leaky tent or Cantor's teepee, depending on the presence or absence of the apex.
 W
WIn mathematics, especially in the area of mathematical analysis known as dynamical systems theory, a linear flow on the torus is a flow on the n-dimensional torus
 W
WIn mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension.
 W
WThe Mosely snowflake is a Sierpiński–Menger type of fractal obtained in two variants either by the operation opposite to creating the Sierpiński-Menger snowflake or Cantor dust i.e. not by leaving but by removing eight of the smaller 1/3-scaled corner cubes and the central one from each cube left from the previous recursion (lighter) or by removing only corner cubes (heavier). In one dimension this operation is trivial and converges only to single point. It resembles the original water snowflake of snow. By the construction the Hausdorff dimension of the lighter snowflake is
 W
WIn real analysis, the projectively extended real line, is the extension of the set of the real numbers, by a point denoted ∞. It is thus the set with the standard arithmetic operations extended where possible, and is sometimes denoted by The added point is called the point at infinity, because it is considered as a neighbour of both ends of the real line. More precisely, the point at infinity is the limit of every sequence of real numbers whose absolute values are increasing and unbounded.
 W
WIn mathematics, a pseudomanifold is a special type of topological space. It looks like a manifold at most of its points, but it may contain singularities. For example, the cone of solutions of forms a pseudomanifold.
 W
WIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set R of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one. It can be thought of as a vector space, a metric space, a topological space, a measure space, or a linear continuum.
 W
WIn mathematics, a rose is a topological space obtained by gluing together a collection of circles along a single point. The circles of the rose are called petals. Roses are important in algebraic topology, where they are closely related to free groups.
 W
WThe Sierpiński carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is one generalization of the Cantor set to two dimensions; another is the Cantor dust.
 W
WThe Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.
 W
WIn mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex.
 W
WIn topology, the Sorgenfrey plane is a frequently-cited counterexample to many otherwise plausible-sounding conjectures. It consists of the product of two copies of the Sorgenfrey line, which is the real line under the half-open interval topology. The Sorgenfrey line and plane are named for the American mathematician Robert Sorgenfrey.