 W
WIn graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the order of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph is perfect if and only if for all we have .
 W
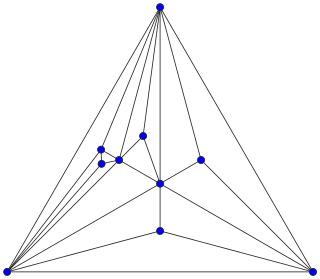
WIn combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.
 W
WIn graph theory, a branch of combinatorial mathematics, a block graph or clique tree is a type of undirected graph in which every biconnected component (block) is a clique.
 W
WIn the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.
 W
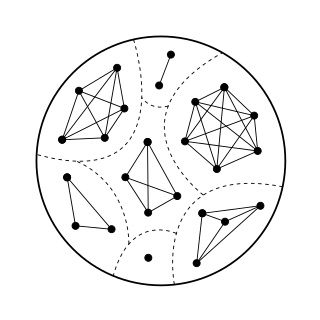
WIn graph theory, a branch of mathematics, a cluster graph is a graph formed from the disjoint union of complete graphs. Equivalently, a graph is a cluster graph if and only if it has no three-vertex induced path; for this reason, the cluster graphs are also called P3-free graphs. They are the complement graphs of the complete multipartite graphs and the 2-leaf powers.
 W
WIn graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
 W
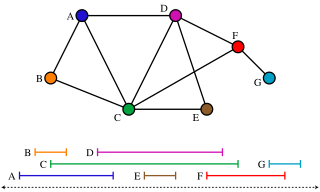
WIn graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.
 W
WIn graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.
 W
WIn graph theory, a k-tree is an undirected graph formed by starting with a (k + 1)-vertex complete graph and then repeatedly adding vertices in such a way that each added vertex v has exactly k neighbors U such that, together, the k + 1 vertices formed by v and U form a clique.
 W
WIn the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
 W
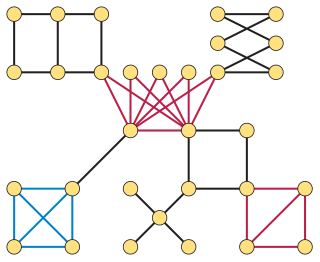
WIn the mathematical area of graph theory, a k-leaf power of a tree is a graph whose vertices are the leaves of and whose edges connect pairs of leaves whose distance in is at most . That is, is an induced subgraph of the graph power , induced by the leaves of . For a graph constructed in this way, is called a k-leaf root of .
 W
WIn graph theory, a line perfect graph is a graph whose line graph is a perfect graph. Equivalently, these are the graphs in which every odd-length simple cycle is a triangle.
 W
WIn graph theory, a Meyniel graph is a graph in which every odd cycle of length five or more has at least two chords, edges connecting non-consecutive vertices of the cycle. The chords may be uncrossed or they may cross each other, as long as there are at least two of them.
 W
WIn graph theory, a parity graph is a graph in which every two induced paths between the same two vertices have the same parity: either both paths have odd length, or both have even length. This class of graphs was named and first studied by Burlet & Uhry (1984).
 W
WIn mathematics, a permutation graph is a graph whose vertices represent the elements of a permutation, and whose edges represent pairs of elements that are reversed by the permutation. Permutation graphs may also be defined geometrically, as the intersection graphs of line segments whose endpoints lie on two parallel lines. Different permutations may give rise to the same permutation graph; a given graph has a unique representation if it is prime with respect to the modular decomposition.
 W
WIn graph theory, a Ptolemaic graph is an undirected graph whose shortest path distances obey Ptolemy's inequality, which in turn was named after the Greek astronomer and mathematician Ptolemy. The Ptolemaic graphs are exactly the graphs that are both chordal and distance-hereditary; they include the block graphs and are a subclass of the perfect graphs.
 W
WIn graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and each edge represents a legal move from one square to another. The same graphs can be defined mathematically as the Cartesian products of two complete graphs or as the line graphs of complete bipartite graphs.
 W
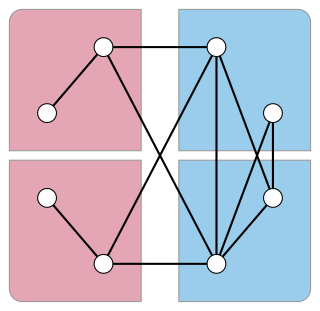
WIn graph theory, a skew partition of a graph is a partition of its vertices into two subsets, such that the induced subgraph formed by one of the two subsets is disconnected and the induced subgraph formed by the other subset is the complement of a disconnected graph. Skew partitions play an important role in the theory of perfect graphs.
 W
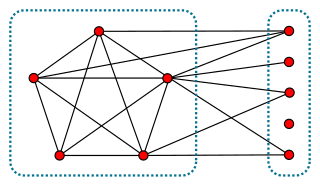
WIn graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set. Split graphs were first studied by Földes and Hammer, and independently introduced by Tyshkevich and Chernyak (1979).
 W
WIn graph theory, a threshold graph is a graph that can be constructed from a one-vertex graph by repeated applications of the following two operations:Addition of a single isolated vertex to the graph. Addition of a single dominating vertex to the graph, i.e. a single vertex that is connected to all other vertices.
 W
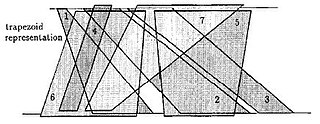
WIn graph theory, trapezoid graphs are intersection graphs of trapezoids between two horizontal lines. They are a class of co-comparability graphs that contain interval graphs and permutation graphs as subclasses. A graph is a trapezoid graph if there exists a set of trapezoids corresponding to the vertices of the graph such that two vertices are joined by an edge if and only if the corresponding trapezoids intersect. Trapezoid graphs were introduced by Dagan, Golumbic, and Pinter in 1988. There exists algorithms for chromatic number, weighted independent set, clique cover, and maximum weighted clique.
 W
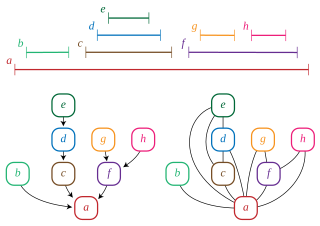
WIn graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques. Trivially perfect graphs were first studied by but were named by Golumbic (1978); Golumbic writes that "the name was chosen since it is trivial to show that such a graph is perfect." Trivially perfect graphs are also known as comparability graphs of trees, arborescent comparability graphs, and quasi-threshold graphs.
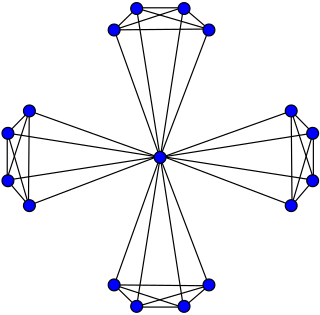 W
WIn the mathematical field of graph theory, the windmill graph Wd(k,n) is an undirected graph constructed for k ≥ 2 and n ≥ 2 by joining n copies of the complete graph Kk at a shared universal vertex. That is, it is a 1-clique-sum of these complete graphs.