24 Permutations

In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set.

The 15 puzzle is a sliding puzzle that consists of a frame of numbered square tiles in random order with one tile missing. The puzzle also exists in other sizes, particularly the smaller 8 puzzle. If the size is 3×3 tiles, the puzzle is called the 8 puzzle or 9 puzzle, and if 4×4 tiles, the puzzle is called the 15 puzzle or 16 puzzle named, respectively, for the number of tiles and the number of spaces. The goal of the puzzle is to place the tiles in order by making sliding moves that use the empty space.

The 100 prisoners problem is a mathematical problem in probability theory and combinatorics. In this problem, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive. The rules state that each prisoner may open only 50 drawers and cannot communicate with other prisoners. At first glance, the situation appears hopeless, but a clever strategy offers the prisoners a realistic chance of survival. Danish computer scientist Peter Bro Miltersen first proposed the problem in 2003.

Change ringing is the art of ringing a set of tuned bells in a tightly controlled manner to produce precise variations in their successive striking sequences, known as "changes". This can be by method ringing in which the ringers commit to memory the rules for generating each change, or by call changes, where the ringers are instructed how to generate each change by instructions from a conductor. This creates a form of bell music which cannot be discerned as a conventional melody, but is a series of mathematical sequences.

A circular permutation is a relationship between proteins whereby the proteins have a changed order of amino acids in their peptide sequence. The result is a protein structure with different connectivity, but overall similar three-dimensional (3D) shape. In 1979, the first pair of circularly permuted proteins – concanavalin A and lectin – were discovered; over 2000 such proteins are now known.

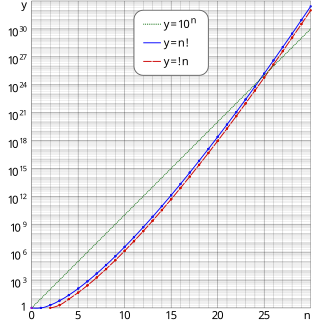
In mathematics, the cycles of a permutation π of a finite set S correspond bijectively to the orbits of the subgroup generated by π acting on S. These orbits are subsets of S that can be written as { c1, ..., cl }, such thatπ(ci) = ci + 1 for i = 1, ..., l − 1, and π(cl) = c1.

In combinatorial mathematics, a derangement is a permutation of the elements of a set, such that no element appears in its original position. In other words, a derangement is a permutation that has no fixed points.

Ghost Leg, known in Japan as Amidakuji or in Korea as Sadaritagi, is a method of lottery designed to create random pairings between two sets of any number of things, as long as the number of elements in each set is the same. This is often used to distribute things among people, where the number of things distributed is the same as the number of people. For instance, chores or prizes could be assigned fairly and randomly this way.

Heap's algorithm generates all possible permutations of n objects. It was first proposed by B. R. Heap in 1963. The algorithm minimizes movement: it generates each permutation from the previous one by interchanging a single pair of elements; the other n−2 elements are not disturbed. In a 1977 review of permutation-generating algorithms, Robert Sedgewick concluded that it was at that time the most effective algorithm for generating permutations by computer.

In computer science and discrete mathematics, a sequence has an inversion where two of its elements are out of their natural order.

In computer science and mathematics, the Josephus problem is a theoretical problem related to a certain counting-out game.

In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of male-female couples at a round dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas and independently, a few years earlier, by Peter Guthrie Tait in connection with knot theory. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is12, 96, 3120, 115200, 5836320, 382072320, 31488549120, ....

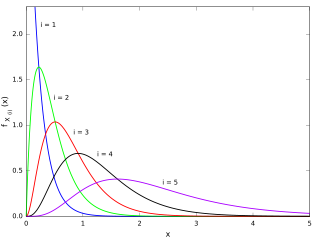
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference.

In music, a permutation (order) of a set is any ordering of the elements of that set. A specific arrangement of a set of discrete entities, or parameters, such as pitch, dynamics, or timbre. Different permutations may be related by transformation, through the application of zero or more operations, such as transposition, inversion, retrogradation, circular permutation, or multiplicative operations. These may produce reorderings of the members of the set, or may simply map the set onto itself.

In cryptography, a permutation box is a method of bit-shuffling used to permute or transpose bits across S-boxes inputs, retaining diffusion while transposing.

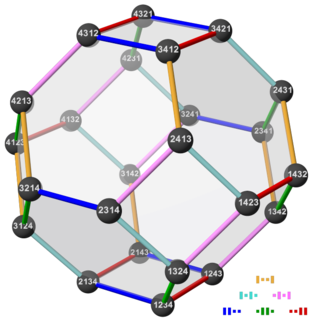
In mathematics, the permutohedron of order n is an (n − 1)-dimensional polytope embedded in an n-dimensional space. Its vertex coordinates (labels) are the permutations of the first n natural numbers. The edges identify the shortest possible paths that connect two vertices (permutations). Two permutations connected by an edge differ in only two places, and the numbers on these places are neighbors.

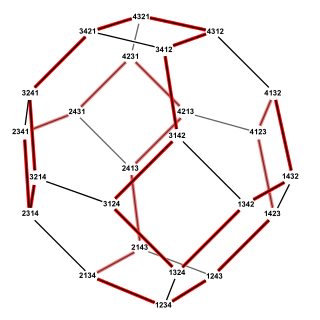
The Steinhaus–Johnson–Trotter algorithm or Johnson–Trotter algorithm, also called plain changes, is an algorithm named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter that generates all of the permutations of n elements. Each permutation in the sequence that it generates differs from the previous permutation by swapping two adjacent elements of the sequence. Equivalently, this algorithm finds a Hamiltonian cycle in the permutohedron.

In mathematics, particularly in combinatorics, a Stirling number of the second kind is the number of ways to partition a set of n objects into k non-empty subsets and is denoted by or . Stirling numbers of the second kind occur in the field of mathematics called combinatorics and the study of partitions.

In combinatorial mathematics, a Stirling permutation of order k is a permutation of the multiset 1, 1, 2, 2, ..., k, k with the additional property that, for each value i appearing in the permutation, the values between the two copies of i are larger than i. For instance, the 15 Stirling permutations of order three are1,1,2,2,3,3; 1,2,2,1,3,3; 2,2,1,1,3,3; 1,1,2,3,3,2; 1,2,2,3,3,1; 2,2,1,3,3,1; 1,1,3,3,2,2; 1,2,3,3,2,1; 2,2,3,3,1,1; 1,3,3,1,2,2; 1,3,3,2,2,1; 2,3,3,2,1,1; 3,3,1,1,2,2; 3,3,1,2,2,1; 3,3,2,2,1,1.

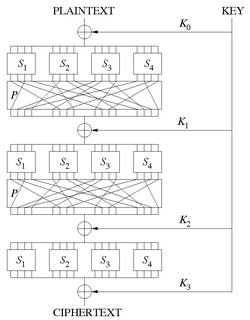
In cryptography, an SP-network, or substitution–permutation network (SPN), is a series of linked mathematical operations used in block cipher algorithms such as AES (Rijndael), 3-Way, Kalyna, Kuznyechik, PRESENT, SAFER, SHARK, and Square.

In combinatorial mathematics, a superpermutation on n symbols is a string that contains each permutation of n symbols as a substring. While trivial superpermutations can simply be made up of every permutation listed together, superpermutations can also be shorter because overlap is allowed. For instance, in the case of n = 2, the superpermutation 1221 contains all possible permutations, but the shorter string 121 also contains both permutations.

In mathematics, the telephone numbers or the involution numbers are a sequence of integers that count the ways n telephone lines can be connected to each other, where each line can be connected to at most one other line. These numbers also describe the number of matchings of a complete graph on n vertices, the number of permutations on n elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with n cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, ....

Veronese bellringing art is a style of ringing church bells that developed around Verona, Italy from the eighteenth century. The bells are rung full circle, being held up by a rope and wheel until a note is required.